P3521 ROT-Tree Rotations

发表于 分类于 阅读次数： Waline： 本文字数： 695 阅读时长 ≈ 2 分钟

考点

  • 线段树合并
  • 逆序对

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 50;
typedef long long ll;
int n, in;
int cnt, lc[maxn * 20], rc[maxn * 20], sz[maxn * 20];
// u：不交换子树
// v：交换子树
ll ans, u, v;

int merge(int p, int q, int l, int r) {
  if (!p || !q) return p + q;
  if (l == r) {
    sz[p] += sz[q];
    return p;
  }
  int mid = (l + r) >> 1;
  u += 1ll * sz[rc[p]] * sz[lc[q]];
  v += 1ll * sz[lc[p]] * sz[rc[q]];
  lc[p] = merge(lc[p], lc[q], l, mid);
  rc[p] = merge(rc[p], rc[q], mid + 1, r);
  sz[p] = sz[lc[p]] + sz[rc[p]];
  return p;
}

void update(int &p, int l, int r, int x) {
  if (!p) p = ++cnt;
  if (l == r) {
    sz[p] += 1;
    return;
  }
  int mid = (l + r) >> 1;
  if (x <= mid)
    update(lc[p], l, mid, x);
  else
    update(rc[p], mid + 1, r, x);
  sz[p] = sz[lc[p]] + sz[rc[p]];
}

void dfs(int &p) {
  scanf("%d", &in);
  if (!in) {
    int lp = 0, rp = 0;
    dfs(lp), dfs(rp);
    u = 0, v = 0;
    p = merge(lp, rp, 1, n);
    ans += min(u, v);
  } else {
    update(p, 1, n, in);
  }
}

int main() {
  scanf("%d", &n);
  int x = 0;
  dfs(x);
  cout << ans << endl;
  return 0;
}

思路

通过观察可以发现，子树之间的交换并不会影响到父树，如图所示：

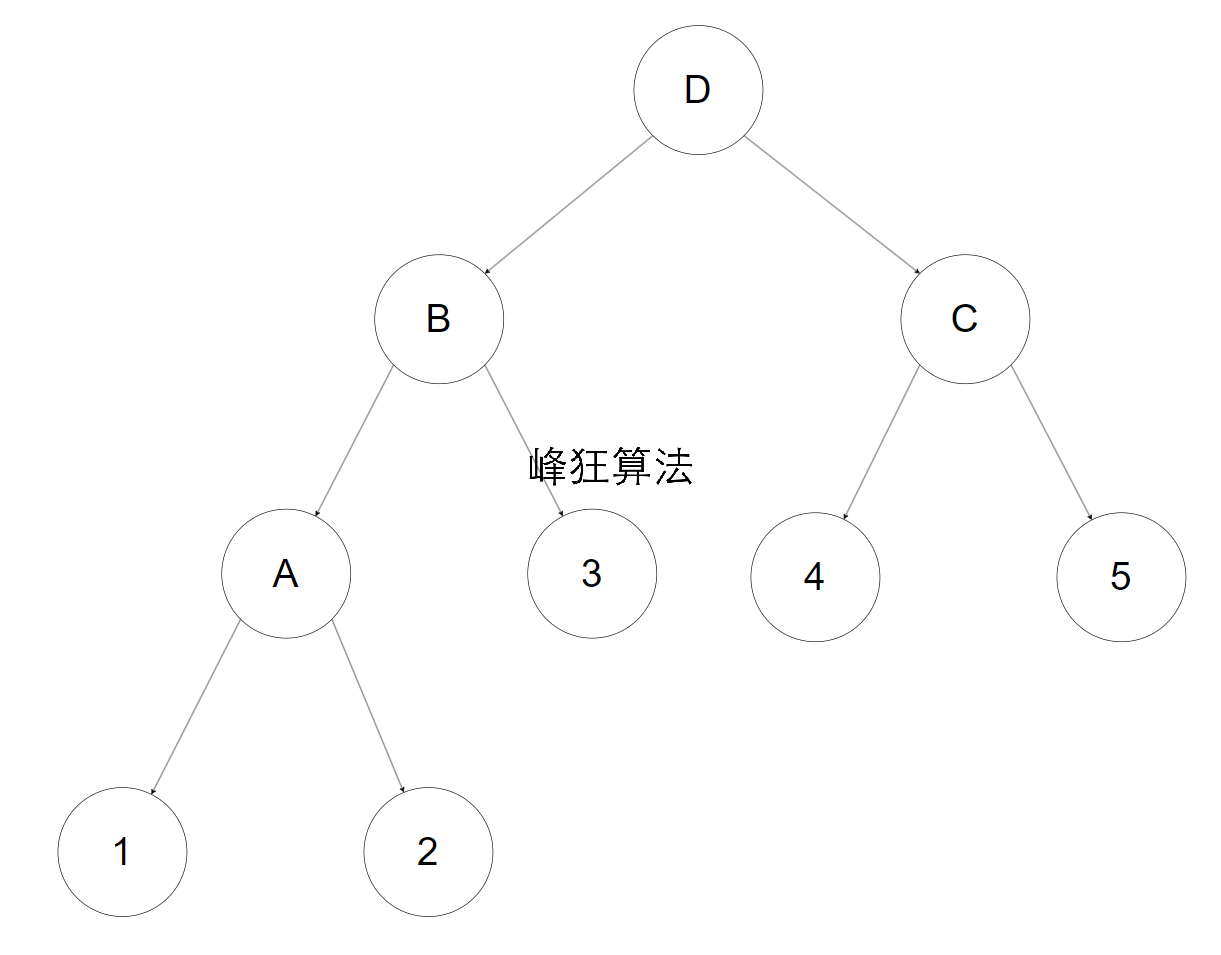
交换A的子树，会影响后续345的逆序对吗？并不会。

交换C的子树，会影响前面123的逆序对吗？也不会。

交换B的子树，会影响后续45的逆序对吗？还是不会，但是会影响A和3的逆序对。

所以总的思路出来了：

自底向上，枚举所有节点，其交换、或不交换子树得到的逆序对个数，取二者较小值为结果，所有节点的结果求和就得到了答案。

由于需要知道每个点的俩子树值域组成，且题目也说值域只有2e5，那么对每个点开权值线段树，向父结点依次合并即可。

现在的关键是，我知道左、右子树的权值线段树，怎样计算左子树对右子树的逆序对贡献呢？

假设当前有序列12345 12345，当前结点区间为[1, 10]，那么左子树区间为[1, 5]，右子树区间为[6, 10]，

在两子树的线段树合并过程中可以发现，逆序对可以即时得出。

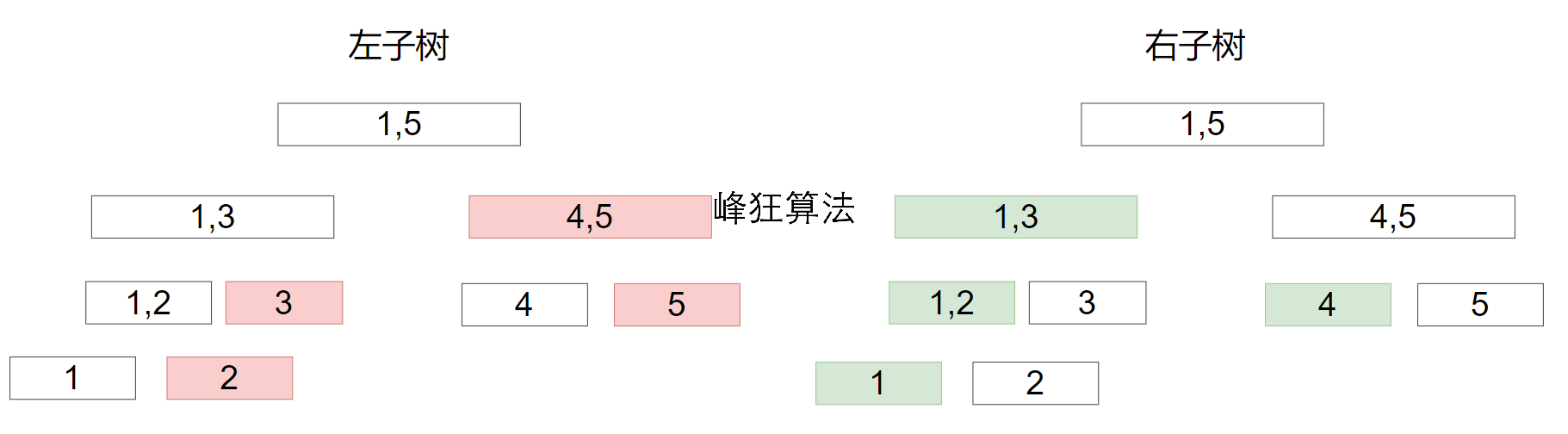
每一层的红色区域个数 * 绿色区域个数就等于该层的逆序对贡献，也就是左子树的右孩子 * 右子树的左孩子；

我们自上而下看看。

左子树的4、5肯定对右子树的[1, 3]有贡献；

左子树的3也对右子树的[1, 2]有贡献，左子树的5也对右子树的4有贡献；

左子树的2也对右子树的1有贡献。

自此，左子树对右子树的所有贡献不重不漏地整理完了，非常巧妙！