acwing-351. 树网的核

发表于 分类于 阅读次数： Waline： 本文字数： 2.3k 阅读时长 ≈ 8 分钟

考点

  • 树的直径
  • 二分
  • 单调队列
  • 贪心
  • 双指针
  • 前缀和

题解

见思路

思路

首先证明两个直径的性质。

第一条，多条直径必相交于一点或一条公共路径。

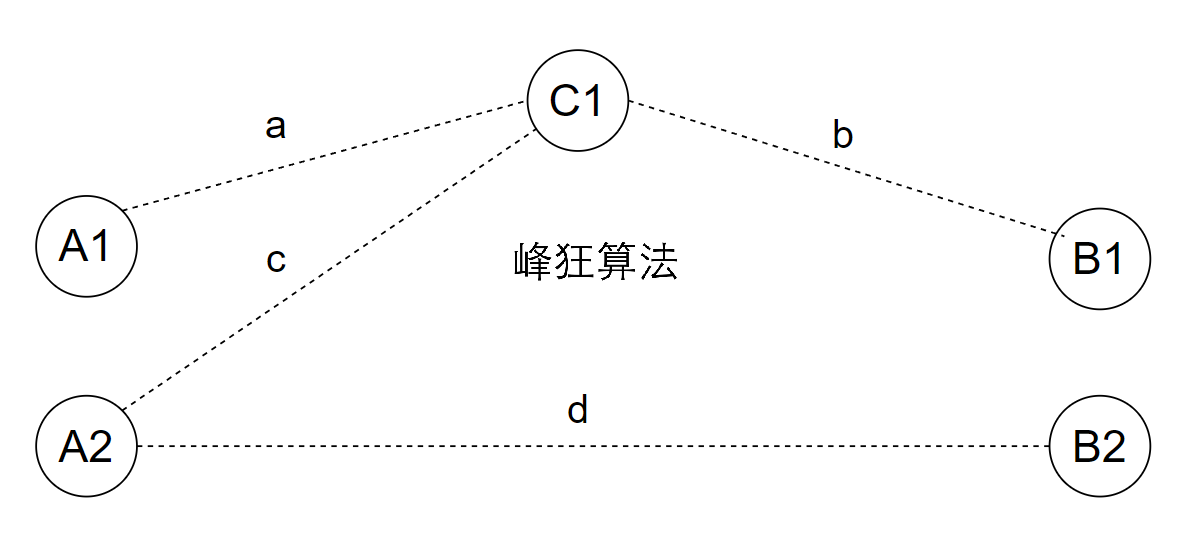
假设A1到B1、A2到B2是两条不相交的直径，分别简写为l1和l2

根据树的连通性原理，A2肯定与l1的某个点C1连通，这样A2才能与A1、B1连通

问题来了，d == a + b，且都是最长长度（因为是直径），那么A1 - C1 - A2 - B2这条路径不是更长吗？！

长度高达a + c + d，相当于a + b + a + c，远大于a + b，

这与直径的定义相悖，得证。

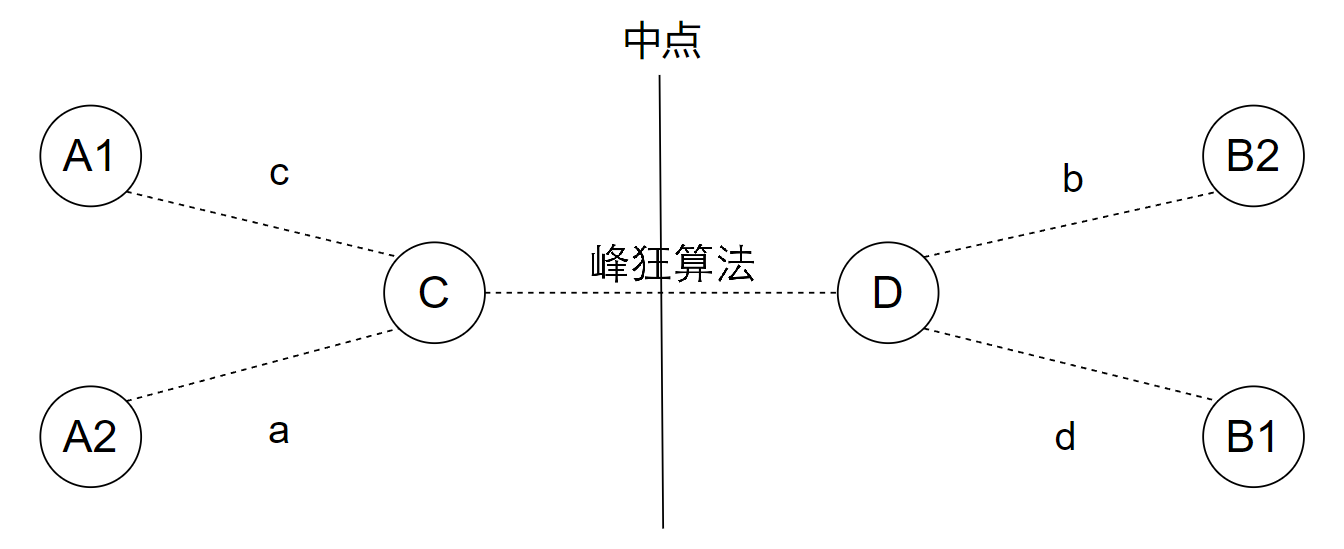
第二条，任意两个同一侧的直径端点到相同直径分叉点的距离均相等。

假设有直径A1 - C - D - B1，还有直径A2 - C - D - B2，CD部分是共有的，长度设为t。

假设不平分，那么假设a > b，d > c，

显然得到a + d + t > b + c + t，也就是A2 - C - D - B1大于A1 - C - D - B2，这与直径的定义相悖。

所以a一定等于c，b也一定等于d。

证毕。

概括一下题意：

选一条直径，直径上选一段路径。

要让全树所有点，到这条路径的最大距离最小

由于本题所有的边权均为非负，那么直径的端点显然只能是叶子节点，否则还能再长。

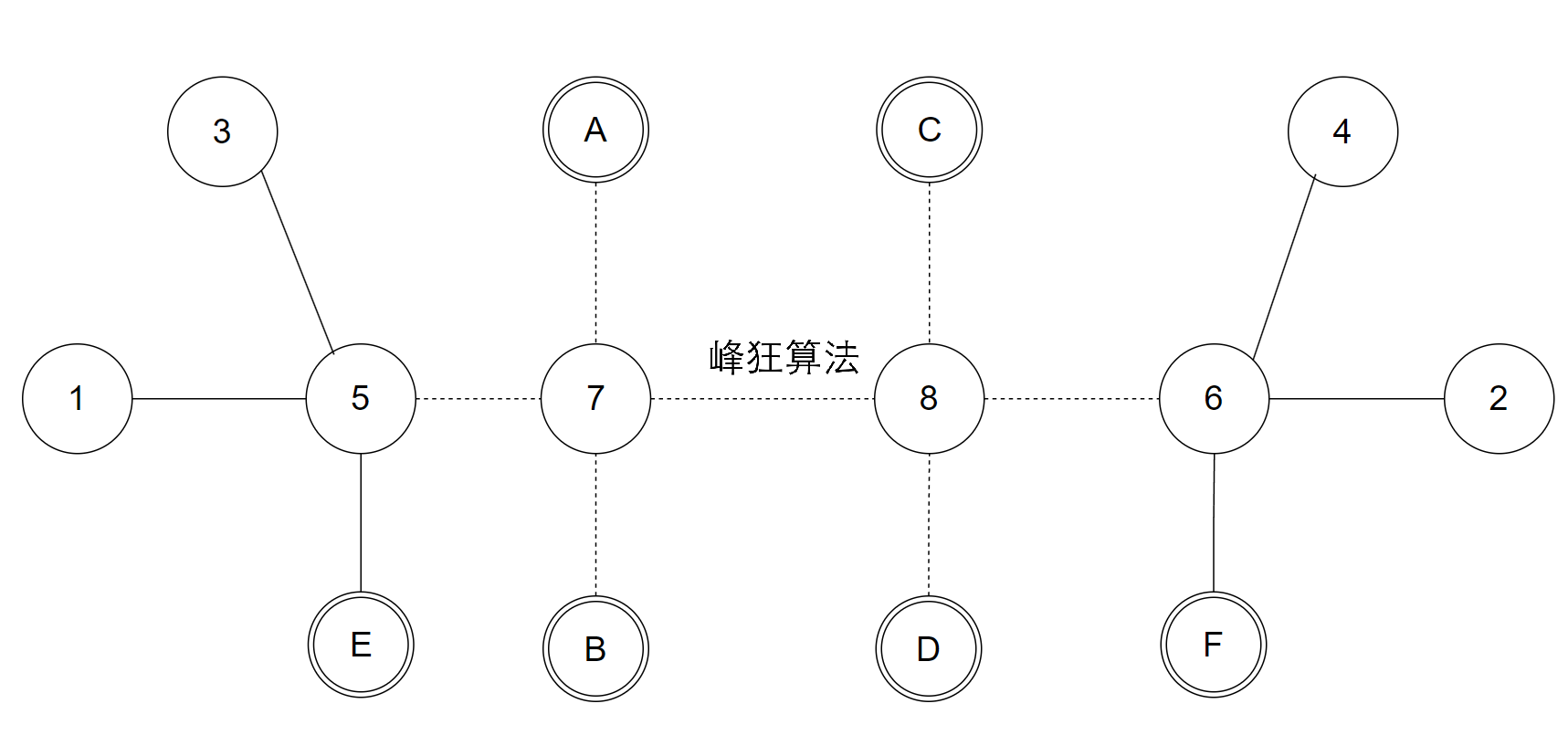
整个树可以抽象如下：

1到2是一条直径，3到4是一条直径，5和6是直径分叉点，ABCDEF均为子树。

结合上述两条性质，选哪条直径对最大距离压根没有影响....

因为1 - 5和3 - 5距离完全相同，2 - 6和4 - 6距离也完全相同，其余子树都接在直径们的公共路径上。

所以直接两次BFS求出任意一条直径即可拿来做文章。

二分

最大值最小显然符合二分的性质，考虑验证条件。

设最大距离为mid，如果每个点到所选路径的最大距离都不会超过mid，验证成功。

设直径的两端点分别为p和q，令它俩各向内收缩mid距离，分别到达点u和v，作图所示。

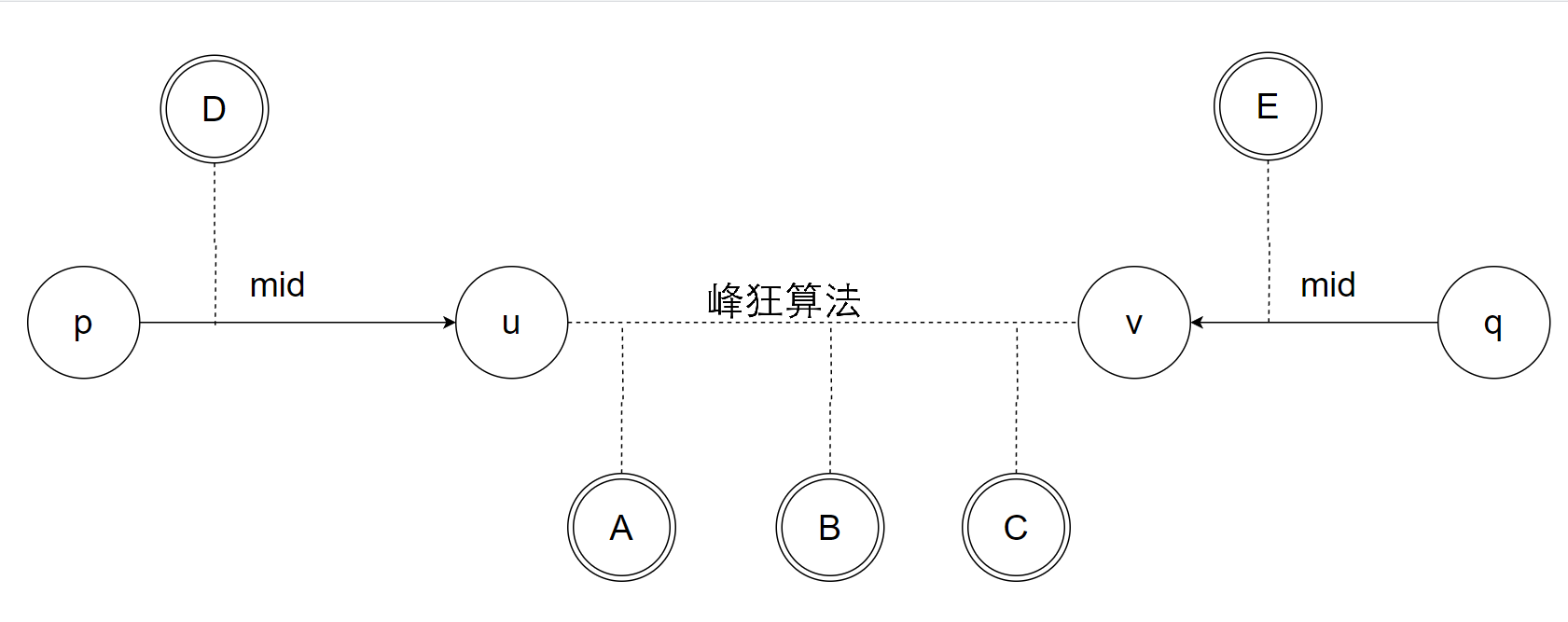
  1. 如果u - v路径长度大于s，说明不满足题意。

  2. 子树D在p - u路径上，子树E在q - v路径上，

    那么D或E的任意点到u - v的路径长度都不可能大于mid，否则D 或 E - u - v - q能成为新的直径。

    换句话说，p和q尽量向内收缩的过程中，顺带还能确保所经路径上的其他子树的最大距离不会超过mid！

    所以，如果u > v，说明两侧子树到直径的任意子路径的最大长度都不会超过mid

  3. 如果u < v且u - v长度小于s，说明u - v这一段路径的子树的最大长度还需我们验证。

    （根据第2条，p - u和q - v两条路径中的子树的最大长度必小于mid，无须验证）

    我们把直径上的所有点都设置为已访问，然后令u - v这条路径上的所有点执行dfs求该点能到的最远距离，

    这样就能找到图上A、B、C等子树到u - v的最远距离了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 50, maxm = 1e6 + 50;
int n, s, tot = 1, head[maxm], ver[maxm], edge[maxm], nxt[maxm];
ll d[maxm], id[maxm];
bool v[maxm];
vector<pair<ll, ll>> path;

void add(int x, int y, int z) {
  ver[++tot] = y, edge[tot] = z, nxt[tot] = head[x], head[x] = tot;
}

int bfs(int bg) {
  queue<int> q;
  memset(d, -1, sizeof(d));
  d[bg] = 0, q.push(bg);
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    for (int i = head[x]; i; i = nxt[i]) {
      int y = ver[i];
      if (~d[y]) continue;
      q.push(y);
      d[y] = d[x] + edge[i];
      id[y] = i;
    }
  }
  int ed = bg;
  for (int i = 1; i <= n; ++i) {
    if (d[i] > d[ed]) ed = i;
  }
  return ed;
}

void route(int p, int q) {
  while (q != p) {
    path.push_back({q, d[q]});
    q = ver[id[q] ^ 1];
  }
  path.push_back({q, d[q]});
}

void mx_dis(ll x) {
  v[x] = 1;
  for (ll i = head[x]; i; i = nxt[i]) {
    ll y = ver[i];
    if (v[y]) continue;
    mx_dis(y);
    d[x] = max(d[x], d[y] + edge[i]);
  }
}

bool check(ll mid) {
  ll p = 0, q = path.size() - 1;
  // p向中间走，假设停到u
  while (p + 1 < path.size() && path[p + 1].second <= mid) ++p;
  // q向中间走，假设停到v
  while (q - 1 >= 0 && path.back().second - path[q - 1].second <= mid) --q;
  // p > q，说明直径两端所有的子树到uv路径的距离都小于mid
  if (p > q) return 1;
  // uv路径长度大于s，不满足题意
  if (path[q].second - path[p].second > s) return 0;
  memset(v, 0, sizeof(v)), memset(d, 0, sizeof(d));
  // 直径所有点都设为已访问
  // 求“直径上的点到其他子树的最远距离”就不会经过直径了
  for (int i = 0; i < path.size(); ++i) v[path[i].first] = 1;
  for (int i = p; i <= q; ++i) {
    mx_dis(path[i].first);
    if (d[path[i].first] > mid) return 0;
  }
  return 1;
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0);
  cin >> n >> s;
  ll sum = 0;
  for (int x, y, z, i = 1; i < n; ++i) {
    cin >> x >> y >> z;
    add(x, y, z), add(y, x, z);
    sum += z;
  }
  // 寻找任意一条直径
  int p = bfs(1), q = bfs(p);
  // 保存整条直径
  route(p, q);
  reverse(path.begin(), path.end());
  ll l = 0, r = sum;
  while (l <= r) {
    ll mid = (l + r) / 2;
    if (check(mid))
      r = mid - 1;
    else
      l = mid + 1;
  }
  cout << l << endl;
  return 0;
}

单调队列与暴力

抛开二分，我们直接考虑最大距离最小的情况。

当i、j两个游标在直径上移动时，可以发现，当前的路径最大值取决于以下式子：

max(p到游标i的距离，i到j路径中子树的最大距离，q到游标j的距离)

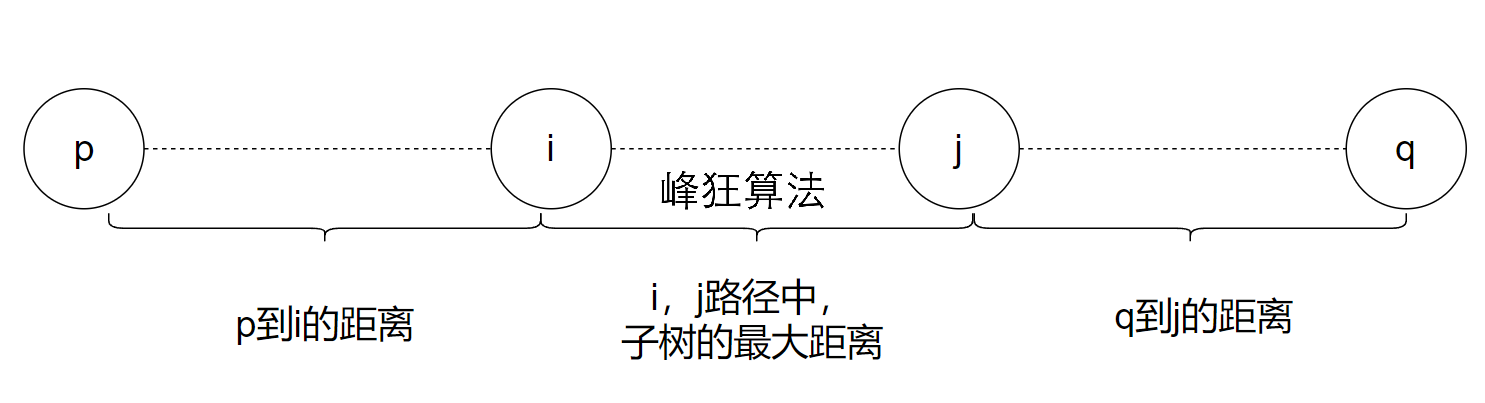
在固定i的情况下，j越大，q到j的距离肯定更小，所以有两种办法：

  1. i与j维护一个单调队列，维护i到j之间子树的最大距离；

    只要i到j的距离不超过s，j就一直向右扩张（贪心思路），在过程中比较上述式子。

  2. 求最大值的运算具有结合律和分配律，两个游标一定会经过直径上的所有子树；

    那倒不如直接暴力求出所有子树的最大距离，是个定值，记为mx_d；

    然后i、j俩游标正常移动，直接比较下述式子即可：

    max(p到游标i的距离，mx_d，q到游标j的距离)

单调队列的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 50, maxm = 1e6 + 50;
int n, s, t, tot = 1, head[maxm], ver[maxm], edge[maxm], nxt[maxm];
int d[maxm], id[maxm];
bool v[maxm];
int hd, tl, a[maxn], b[maxn], sum[maxn], dq[maxn];

void add(int x, int y, int z) {
  ver[++tot] = y, edge[tot] = z, nxt[tot] = head[x], head[x] = tot;
}

int bfs(int bg) {
  queue<int> q;
  memset(d, -1, sizeof(d));
  d[bg] = 0, q.push(bg);
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    for (int i = head[x]; i; i = nxt[i]) {
      int y = ver[i];
      if (~d[y]) continue;
      q.push(y);
      d[y] = d[x] + edge[i];
      id[y] = i;
    }
  }
  int ed = bg;
  for (int i = 1; i <= n; ++i) {
    if (d[i] > d[ed]) ed = i;
  }
  return ed;
}

void route(int p, int q) {
  while (q != p) {
    a[++t] = q;
    b[t + 1] = edge[id[q]];
    q = ver[id[q] ^ 1];
  }
  a[++t] = p;
}

void mx_dis(int x) {
  v[x] = 1;
  for (int i = head[x]; i; i = nxt[i]) {
    int y = ver[i];
    if (v[y]) continue;
    mx_dis(y);
    d[x] = max(d[x], d[y] + edge[i]);
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0);
  cin >> n >> s;
  for (int x, y, z, i = 1; i < n; ++i) {
    cin >> x >> y >> z;
    add(x, y, z), add(y, x, z);
  }
  // 寻找任意一条直径
  int p = bfs(1), q = bfs(p);
  // 保存整条直径
  route(p, q);
  memset(d, 0, sizeof(d));
  for (int i = 1; i <= t; ++i) v[a[i]] = 1;
  for (int i = 1; i <= t; ++i) {
    mx_dis(a[i]);
    // 前缀和优化
    sum[i] = sum[i - 1] + b[i];
  }
  int ans = 0x3f3f3f3f;
  for (int i = 1, j = 1; i <= t; ++i) {
    while (hd < tl && dq[hd] < i) ++hd;
    while (j + 1 <= t && sum[j + 1] - sum[i] <= s) {
      ++j;
      while (hd < tl && d[a[j]] > d[a[dq[tl - 1]]]) --tl;
      dq[tl++] = j;
    }
    ans = min(ans, max(d[a[dq[hd]]], max(sum[i], sum[t] - sum[j])));
  }
  cout << ans << endl;
  return 0;
}

暴力的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 50, maxm = 1e6 + 50;
int n, s, t, tot = 1, head[maxm], ver[maxm], edge[maxm], nxt[maxm];
int d[maxm], id[maxm];
bool v[maxm];
int hd, tl, a[maxn], b[maxn], sum[maxn], dq[maxn];

void add(int x, int y, int z) {
  ver[++tot] = y, edge[tot] = z, nxt[tot] = head[x], head[x] = tot;
}

int bfs(int bg) {
  queue<int> q;
  memset(d, -1, sizeof(d));
  d[bg] = 0, q.push(bg);
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    for (int i = head[x]; i; i = nxt[i]) {
      int y = ver[i];
      if (~d[y]) continue;
      q.push(y);
      d[y] = d[x] + edge[i];
      id[y] = i;
    }
  }
  int ed = bg;
  for (int i = 1; i <= n; ++i) {
    if (d[i] > d[ed]) ed = i;
  }
  return ed;
}

void route(int p, int q) {
  while (q != p) {
    a[++t] = q;
    b[t + 1] = edge[id[q]];
    q = ver[id[q] ^ 1];
  }
  a[++t] = p;
}

void mx_dis(int x) {
  v[x] = 1;
  for (int i = head[x]; i; i = nxt[i]) {
    int y = ver[i];
    if (v[y]) continue;
    mx_dis(y);
    d[x] = max(d[x], d[y] + edge[i]);
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0);
  cin >> n >> s;
  for (int x, y, z, i = 1; i < n; ++i) {
    cin >> x >> y >> z;
    add(x, y, z), add(y, x, z);
  }
  // 寻找任意一条直径
  int p = bfs(1), q = bfs(p);
  // 保存整条直径
  route(p, q);
  memset(d, 0, sizeof(d));
  int mx_d = 0;
  for (int i = 1; i <= t; ++i) v[a[i]] = 1;
  for (int i = 1; i <= t; ++i) {
    mx_dis(a[i]);
    sum[i] = sum[i - 1] + b[i];
    mx_d = max(mx_d, d[a[i]]);
  }
  int ans = 0x3f3f3f3f;
  for (int i = 1, j = 1; i <= t; ++i) {
    while (j + 1 <= t && sum[j + 1] - sum[i] <= s) ++j;
    ans = min(ans, max(mx_d, max(sum[i], sum[t] - sum[j])));
  }
  cout << ans << endl;
  return 0;
}