acwing-350. 巡逻

发表于 分类于 阅读次数： Waline： 本文字数： 811 阅读时长 ≈ 3 分钟

考点

  • 树的直径

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 50, maxm = 2e5 + 50;
int n, m, k, tot = 1, l1, l2, head[maxn], d[maxn];
int ver[maxm], edge[maxm], nxt[maxm];
// 每条边的记号
int id[maxm];
bool v[maxn];

void add(int x, int y, int z) {
  ver[++tot] = y, edge[tot] = z, nxt[tot] = head[x], head[x] = tot;
}

int bfs(int s) {
  queue<int> q;
  // 在树中，点到点之间只有唯一一条路径
  // 所以d数组刚好也作为标志数组
  memset(d, -1, sizeof(d));
  q.push(s);
  d[s] = 0;
  int t = s;
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    if (d[x] > d[t]) t = x;
    for (int i = head[x]; i; i = nxt[i]) {
      int y = ver[i];
      if (~d[y]) continue;
      d[y] = d[x] + edge[i];
      id[y] = i;
      q.push(y);
    }
  }
  return t;
}

void update(int p, int q) {
  while (p != q) {
    edge[id[q]] = -1;
    edge[id[q] ^ 1] = -1;
    q = ver[id[q] ^ 1];
  }
}

void dp(int x) {
  v[x] = 1;
  for (int i = head[x]; i; i = nxt[i]) {
    int y = ver[i];
    if (v[y]) continue;
    dp(y);
    l2 = max(l2, d[x] + d[y] + edge[i]);
    d[x] = max(d[x], d[y] + edge[i]);
  }
}

int main() {
  cin >> n >> k;
  for (int x, y, z, i = 1; i < n; ++i) {
    cin >> x >> y;
    add(x, y, 1), add(y, x, 1);
  }
  int p = bfs(1), q = bfs(p);
  l1 = d[q];
  if (k == 1) {
    cout << 2 * (n - 1) - l1 + 1 << endl;
    return 0;
  }
  // 直径部分取反
  update(p, q);
  memset(d, 0, sizeof(d));
  dp(1);
  cout << 2 * (n - 1) - l1 + 1 - l2 + 1 << endl;
  return 0;
}

思路

在不加路径之前，总的开销是2(n-1)，因为每条路径都必须重复两次。

每加一条路径，路径两端点之间的原路径就会少走一次，新加的路径走一次（题目还说必须只能走一次），

所以选择树中的最长路径（直径）两端点进行连接以达到最佳效果。

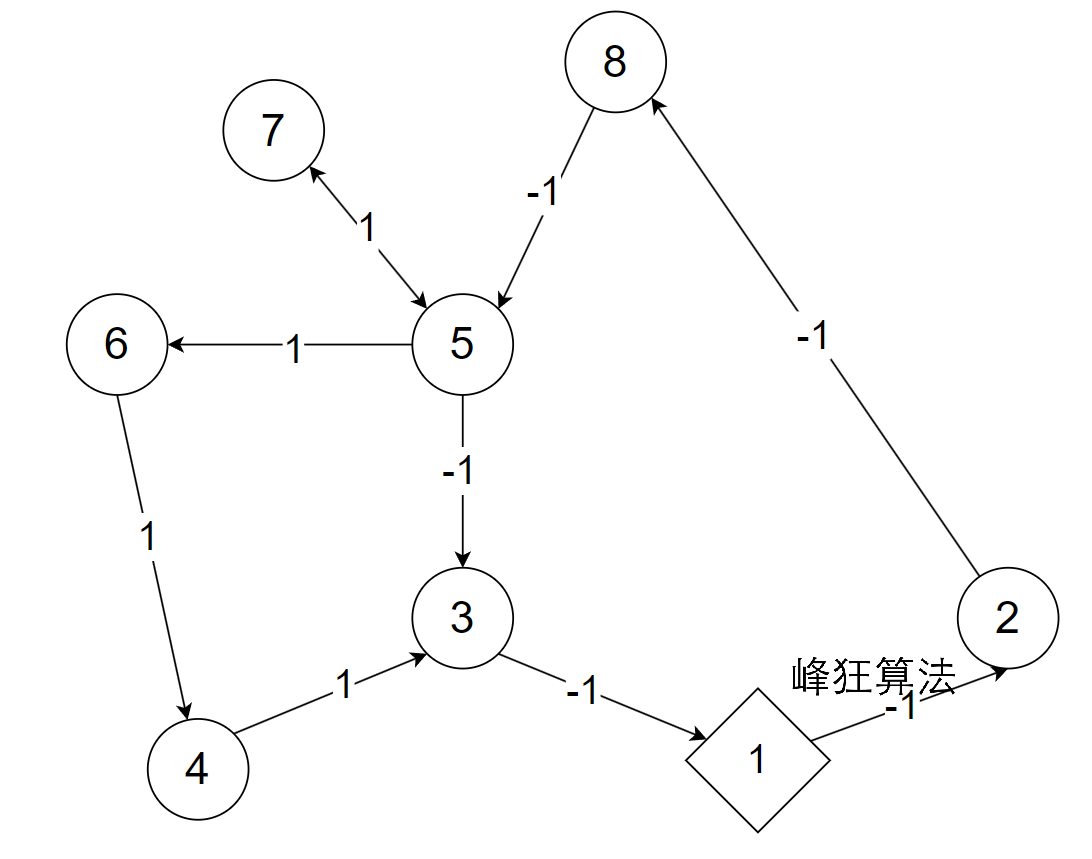
假设原图如下，1为起点，每条路径都要走两次（如箭头所示），直径为2 - 1 - 3 - 5 - 8这一段

这里的边权均为非负，可以使用两次BFS进行求解直径。

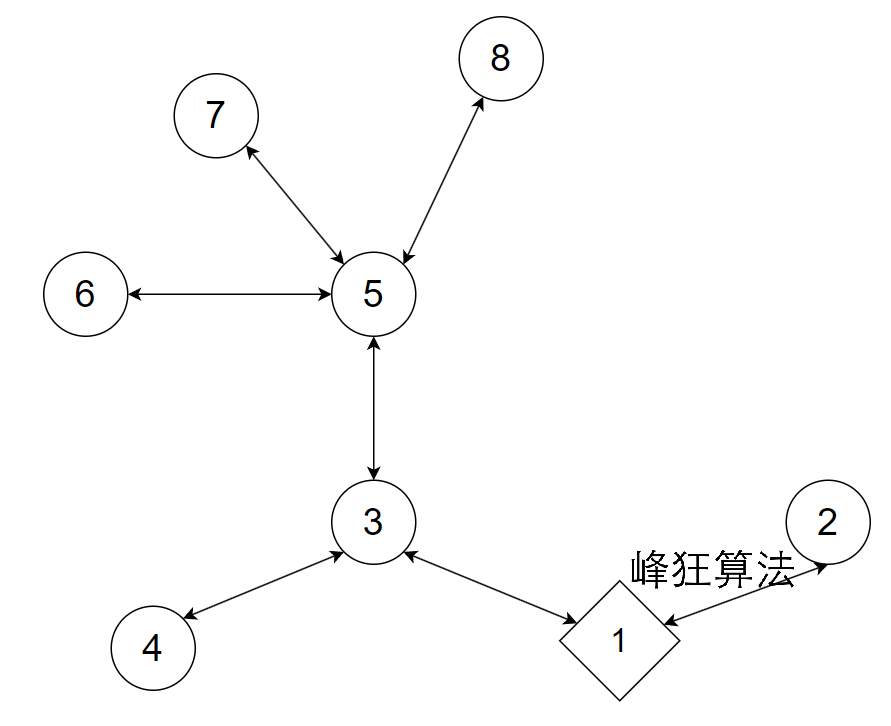
当链接2和8两点后，2 - 1 - 3 - 5 - 8整条直径只需要走一次，

假设这段直径长度为l1，当前的路径开销就是2(n-1) - l1 + 1

将直径部分全部取反，再次寻找新直径（这里只能用树形dp求），会得到以下两种情况：

  1. 新的直径不包含上一条直径的任一条路径。

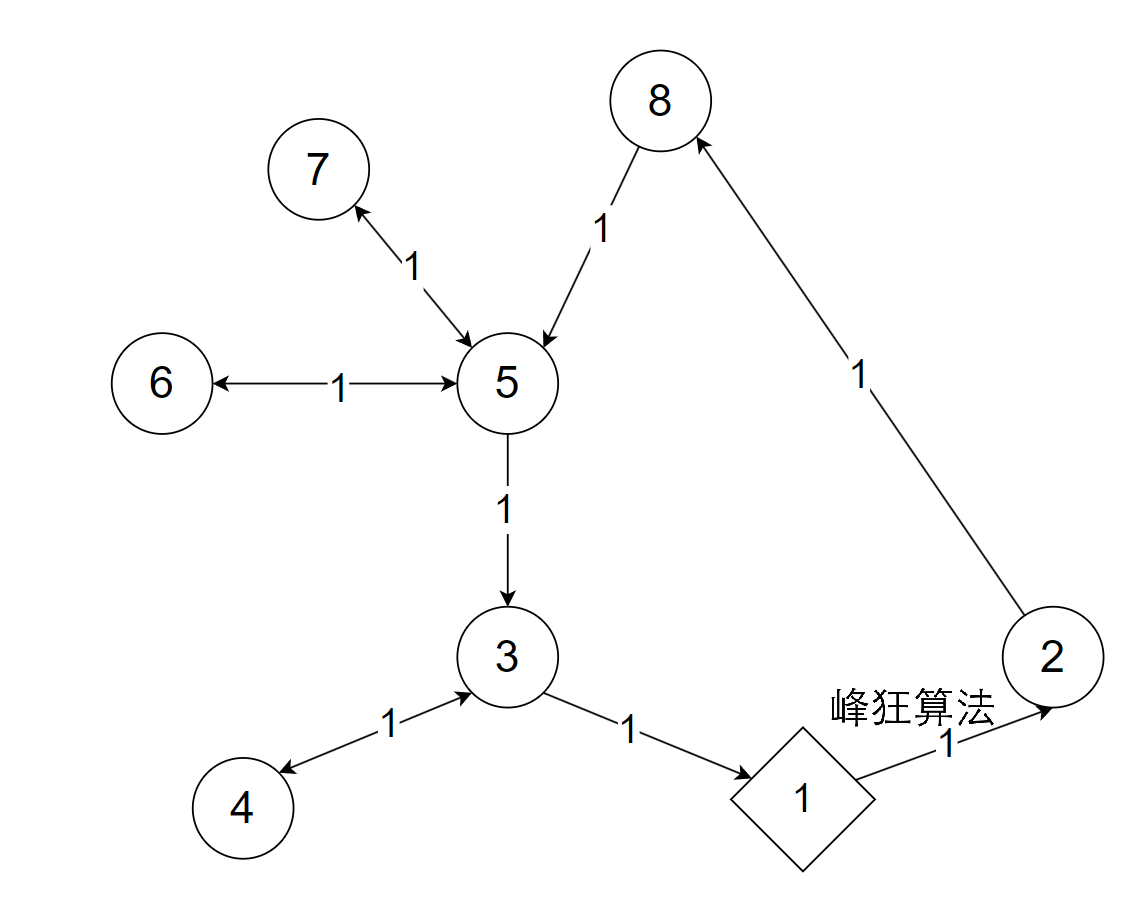
    譬如6 - 5 - 7为新直径，那么将6与7连接建立新路，如图所示。

    假设新直径长度为l2，那么当前路径总开销为2(n-1) - l1 + 1 - l2 + 1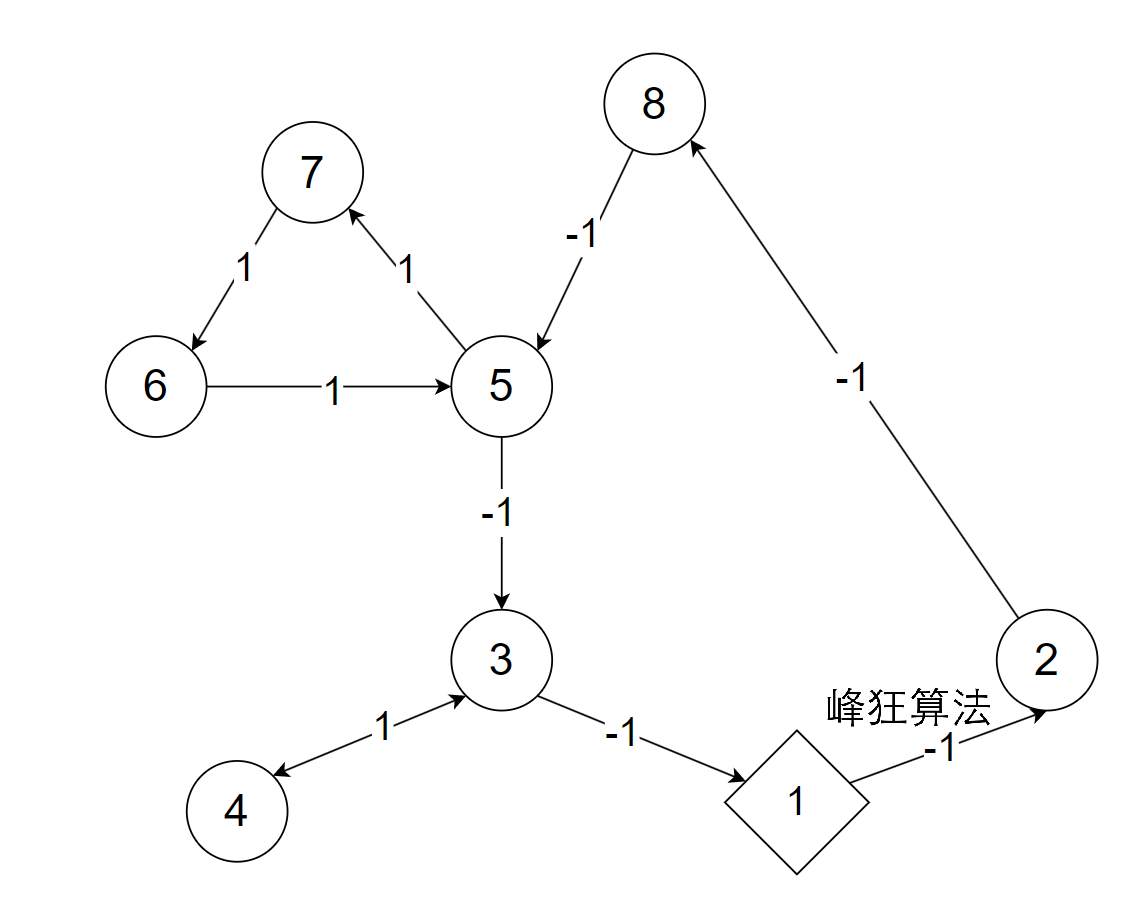

  2. 新的直径包含上一条直径的某一条路径。

    假设新直径为6 - 5 - 3 - 4，连接6与4建立新路，如图所示。

    5 - 3是两条直径的重叠部分，显然任意情况下它一定会被走两次；

    处理第一条直径时，它被计算走了一次，所以这里需要让它再被计算一次，这正是取反的妙处。

    在这里，新直径l2 = 1 (6到5的边权) - 1 (5到3的边权) + 1 (3到4的边权)，

    减去l2不就相当于新直径其它部分正常减去一次，而5 - 3部分再走一次。

    那么当前路径总开销依旧为2(n-1) - l1 + 1 - l2 + 1