acwing-341. 最优贸易

发表于 分类于 阅读次数： Waline： 本文字数： 972 阅读时长 ≈ 3 分钟

考点

  • 最短路
  • 后效性处理

题解

见思路

思路

某一条路径上选p和q两个点，p在前q在后，p买q卖，求最大值。

双向SPFA

很朴素的思路，枚举每个点x作为所有经过它的路径的中点。

正向SPFA从1出发，求到达x的最小点，记为mi[x]；逆向SPFA从n出发，求达到x的最大点，记为mx[x]；

最后找出mx[x] - mi[x]的最大值即可。

之所以不能用dijkstra，是因为找最小、最大点是有后效性，不满足贪心策略的：

比如有5 -> 6，6 -> 7，7 -> 5三条边，假设有mi[5] = 10，然后mi[6] = 5，接着mi[7] = 3，最后mi[5] = 3，5节点完全不可能只出队一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 50, maxm = 5e5 + 50;
// mi[x]：以x为中点的所有路径中，x左侧最小的（包含自己）
// mx[x]：以x为中点的所有路径中，x右侧最大的（包含自己）
int n, m, tot = -1, head[maxn], a[maxn], mi[maxn], mx[maxn];
bool vis[maxn];

struct node {
  int v_, w_, nxt_;
} g[maxm << 1];

void add(int u, int v, int w) {
  g[++tot].v_ = v, g[tot].w_ = w, g[tot].nxt_ = head[u], head[u] = tot;
}

void spfa(int d[], int st, int W) {
  queue<int> q;
  d[st] = a[st], vis[st] = 1, q.push(st);
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    vis[u] = 0;
    for (int i = head[u]; ~i; i = g[i].nxt_) {
      if (g[i].w_ == W || g[i].w_ == 2) {
        int v = g[i].v_, w = g[i].w_;
        int val = W == 1 ? min(d[u], a[v]) : max(d[u], a[v]);
        if (W == 1 && val < d[v] || W == -1 && val > d[v]) {
          d[v] = val;
          if (!vis[v]) {
            vis[v] = 1;
            q.push(v);
          }
        }
      }
    }
  }
}

int main() {
  cin >> n >> m;
  memset(head, -1, sizeof(head));
  // 边权1代表1~n的正向遍历，边权-1代表n~1的反向遍历，边权2代表双向皆可
  for (int i = 1; i <= n; ++i) cin >> a[i];
  for (int u, v, w, i = 1; i <= m; ++i) {
    cin >> u >> v >> w;
    add(u, v, w), add(v, u, w == 1 ? -1 : w);
  }
  memset(mi, 0x3f, sizeof(mi)), memset(vis, 0, sizeof(vis));
  spfa(mi, 1, 1);
  memset(mx, 0xc0, sizeof(mx)), memset(vis, 0, sizeof(vis));
  spfa(mx, n, -1);
  int ans = -1;
  for (int i = 1; i <= n; ++i) ans = max(ans, mx[i] - mi[i]);
  cout << ans;
  return 0;
}

分层图+SPFA

也可以用dp的思路，设D[x, j]代表从1点0层出发，到达x点j层的最大值，有如下转移方程：

  • D[y, j] = max(D[y, j], D[x, j])，同一层边权均为0
  • D[x, j + 1] = max(D[x, j + 1], D[x, j] - a[x])，第0层向第1层转移时，必须先买入商品，边权均为负
  • D[x, j + 1] = max(D[x, j + 1], D[x, j] + a[x])，第1层向第2层转移时，必须卖掉商品赚钱，边权均为正

所以直接对下图用SPFA求最大路，最后输出D[n, 2]即可

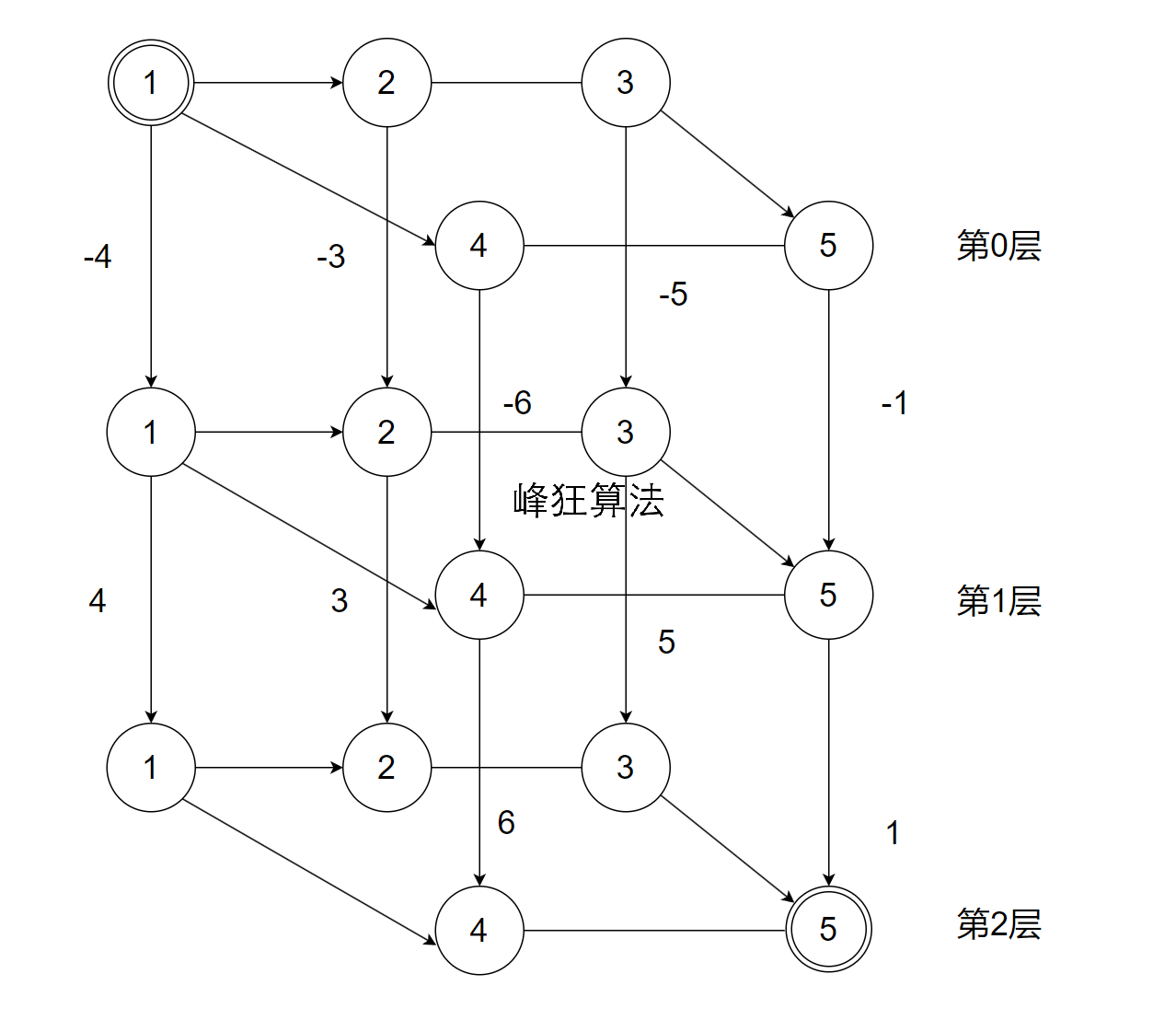
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 50, maxm = 1e6 + 50;
int n, m, tot = -1, head[maxn], a[maxn], d[maxn][3];
bool vis[maxn][3];

struct node {
  int v_, w_, nxt_;
} g[maxm];

void add(int u, int v, int w = 0) {
  g[++tot].v_ = v, g[tot].w_ = w, g[tot].nxt_ = head[u], head[u] = tot;
}

void spfa() {
  memset(d, 0xc0, sizeof(d));
  queue<pair<int, int>> q;
  d[1][0] = 0, vis[1][0] = 1, q.push({1, 0});
  while (!q.empty()) {
    int u = q.front().first, f = q.front().second;
    q.pop();
    vis[u][f] = 0;
    // 同层扩展
    for (int i = head[u]; ~i; i = g[i].nxt_) {
      int v = g[i].v_;
      if (d[v][f] < d[u][f]) {
        d[v][f] = d[u][f];
        if (!vis[v][f]) {
          vis[v][f] = 1;
          q.push({v, f});
        }
      }
    }
    // 第0层向第1层扩展
    if (f == 0 && d[u][f + 1] < d[u][f] - a[u]) {
      d[u][f + 1] = d[u][f] - a[u];
      if (!vis[u][f + 1]) {
        vis[u][f + 1] = 1;
        q.push({u, f + 1});
      }
    }
    // 第1层向第2层扩展
    if (f == 1 && d[u][f + 1] < d[u][f] + a[u]) {
      d[u][f + 1] = d[u][f] + a[u];
      if (!vis[u][f + 1]) {
        vis[u][f + 1] = 1;
        q.push({u, f + 1});
      }
    }
  }
  cout << d[n][2] << endl;
}

int main() {
  cin >> n >> m;
  memset(head, -1, sizeof(head));
  for (int i = 1; i <= n; ++i) cin >> a[i];
  for (int u, v, w, i = 1; i <= m; ++i) {
    cin >> u >> v >> w;
    add(u, v);
    if (w == 2) add(v, u);
  }
  spfa();
  return 0;
}