poj-3662. Telephone Lines

发表于 分类于 阅读次数： Waline： 本文字数： 962 阅读时长 ≈ 3 分钟

考点

  • 后效性处理
  • 最短路
  • 二分
  • 双端队列BFS

题解

见思路

思路

分层图最短路

用动态规划的思想，设D[x, p]表示从1号节点到达基站x，途中已经指定了p条电缆免费时，经过的路径上最贵的电缆的花费最小是多少（选择一条从1到x的路径，使路径上第p + 1大的边权尽量小）。

假设节点x到节点y有一长度为z的无向边，有两种状态转移方式：

  • 该边不免费。

    那么应该用max(D[x, p], z)更新D[y, p]的最小值

  • 该边免费。

    用D[x, p]更新D[y, p + 1]的最小值

通过作图可以发现，若以免费电缆数p分层，整个动态规划的转移其实就是一张分层图：

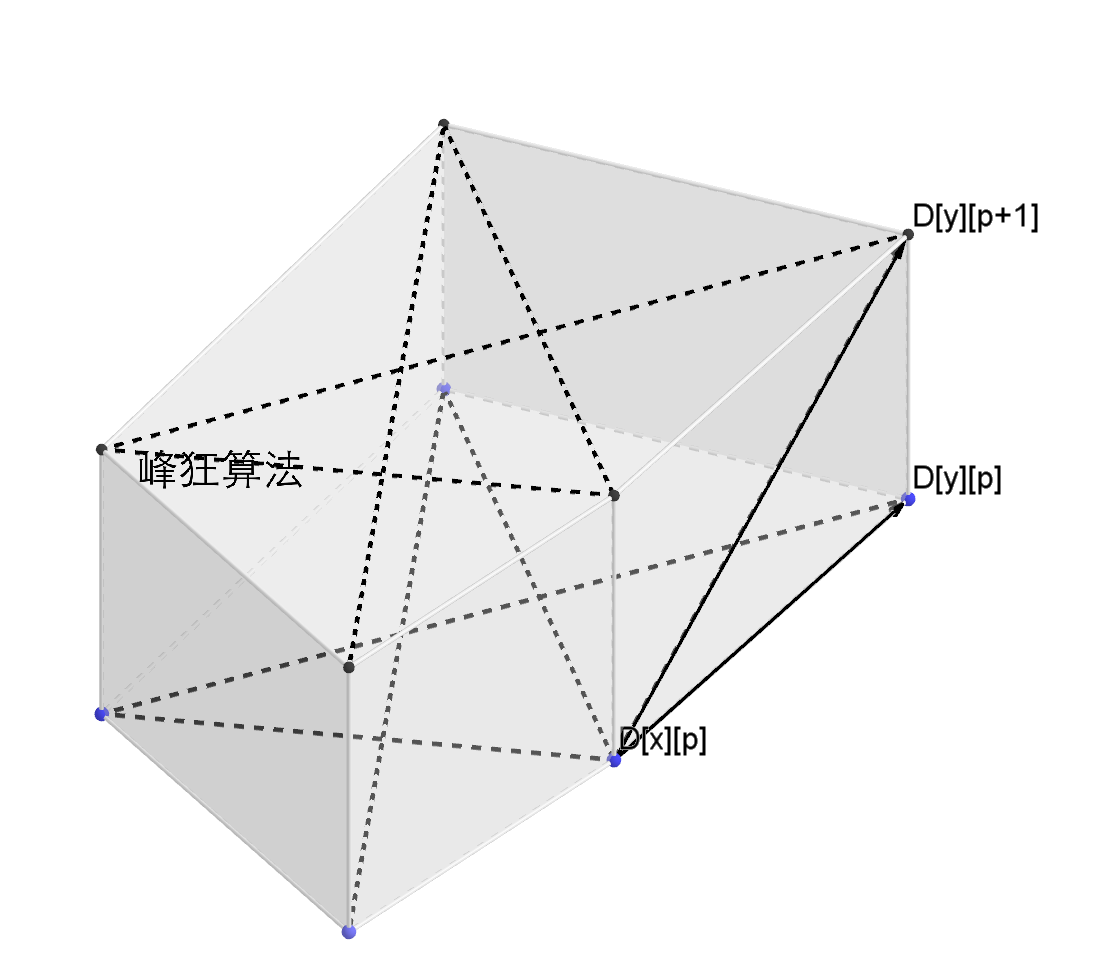
每一层的图可能是有环的，也就是后效性；所以不能按照常规dp的方式做，要套SPFA，直至所有状态收敛。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int maxn = 1e3 + 50, maxm = 1e4 + 50;
int n, p, k, head[maxn], tot = -1, d[maxn][maxn];
bool vis[maxn][maxn];

struct node {
  int v_, w_, nxt_;
} g[maxm << 1];

void add(int u, int v, int w) {
  g[++tot].v_ = v, g[tot].w_ = w, g[tot].nxt_ = head[u], head[u] = tot;
}

void spfa() {
  queue<pair<int, int>> q;
  // d[u][t]：截止到u基站，有t个免费的情况下的最大值最小
  memset(d, 0x7f, sizeof(d));
  q.push(make_pair(1, 0)), d[1][0] = 0, vis[1][0] = 1;
  while (!q.empty()) {
    int u = q.front().first, t = q.front().second;
    q.pop();
    vis[u][t] = 0;
    for (int i = head[u]; ~i; i = g[i].nxt_) {
      int v = g[i].v_, w = g[i].w_;
      if (d[v][t] > max(d[u][t], w)) {
        d[v][t] = max(d[u][t], w);
        if (!vis[v][t]) {
          vis[v][t] = 1;
          q.push(make_pair(v, t));
        }
      }
      if (t < k && d[v][t + 1] > d[u][t]) {
        d[v][t + 1] = d[u][t];
        if (!vis[v][t + 1]) {
          vis[v][t + 1] = 1;
          q.push(make_pair(v, t + 1));
        }
      }
    }
  }
  int ans = 0x7f7f7f7f;
  for (int i = 0; i <= k; ++i) ans = min(ans, d[n][i]);
  cout << (ans == 0x7f7f7f7f ? -1 : ans) << endl;
}

int main() {
  cin >> n >> p >> k;
  memset(head, -1, sizeof(head));
  for (int u, v, w, i = 1; i <= p; ++i) {
    cin >> u >> v >> w;
    add(u, v, w), add(v, u, w);
  }
  spfa();
  return 0;
}

二分 + 双端队列BFS

很难想的二分.........考虑直接枚举第k + 1大的边权mid。

因为必须是k + 1大，应该存在一条路径，大于mid的边权数量必须小于等于k。

如何去在当前图里寻找一条满足条件的路径呢？

把所有升级价格大于mid的电缆看作长度为1的边，小于等于mid的电缆看作长度为0的边，然后求1到n的最短路是否小于等于k即可，01边权的最短路使用双端队列BFS进行求解。

如果最短路的开销小于等于k，说明至少有一条路（最短路）满足条件，就可以继续向左边界收缩；

如果最短路的开销都大于k，说明当前mid太小了，比mid大的数超过了k个，需要向右边界扩张。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <cstring>
#include <deque>
#include <iostream>
using namespace std;
const int maxn = 1e3 + 50, maxm = 1e4 + 50;
int n, p, k, head[maxn], tot = -1, d[maxn];
bool vis[maxn];
deque<int> q;

struct node {
  int v_, w_, nxt_;
} g[maxm << 1];

void add(int u, int v, int w) {
  g[++tot].v_ = v, g[tot].w_ = w, g[tot].nxt_ = head[u], head[u] = tot;
}

bool check(int mid) {
  memset(d, 0x3f, sizeof(d)), memset(vis, 0, sizeof(vis));
  d[1] = 0, q.push_back(1);
  while (!q.empty()) {
    int u = q.front();
    q.pop_front();
    if (vis[u]) continue;
    vis[u] = 1;
    for (int i = head[u]; ~i; i = g[i].nxt_) {
      int v = g[i].v_, w = g[i].w_ > mid;
      if (d[v] > d[u] + w) {
        d[v] = d[u] + w;
        if (w)
          q.push_back(v);
        else
          q.push_front(v);
      }
    }
  }
  return d[n] <= k;
}

int main() {
  cin >> n >> p >> k;
  memset(head, -1, sizeof(head));
  for (int u, v, w, i = 1; i <= p; ++i) {
    cin >> u >> v >> w;
    add(u, v, w), add(v, u, w);
  }
  int l = 0, r = 1e6;
  while (l <= r) {
    int mid = (l + r) / 2;
    if (check(mid))
      r = mid - 1;
    else
      l = mid + 1;
  }
  cout << (l > 1e6 ? -1 : l) << endl;
  return 0;
}