acwing-174.推箱子

发表于 分类于 阅读次数： Waline： 本文字数： 912 阅读时长 ≈ 3 分钟

考点

  • 双重BFS
  • 最短路
  • 分层图

题解

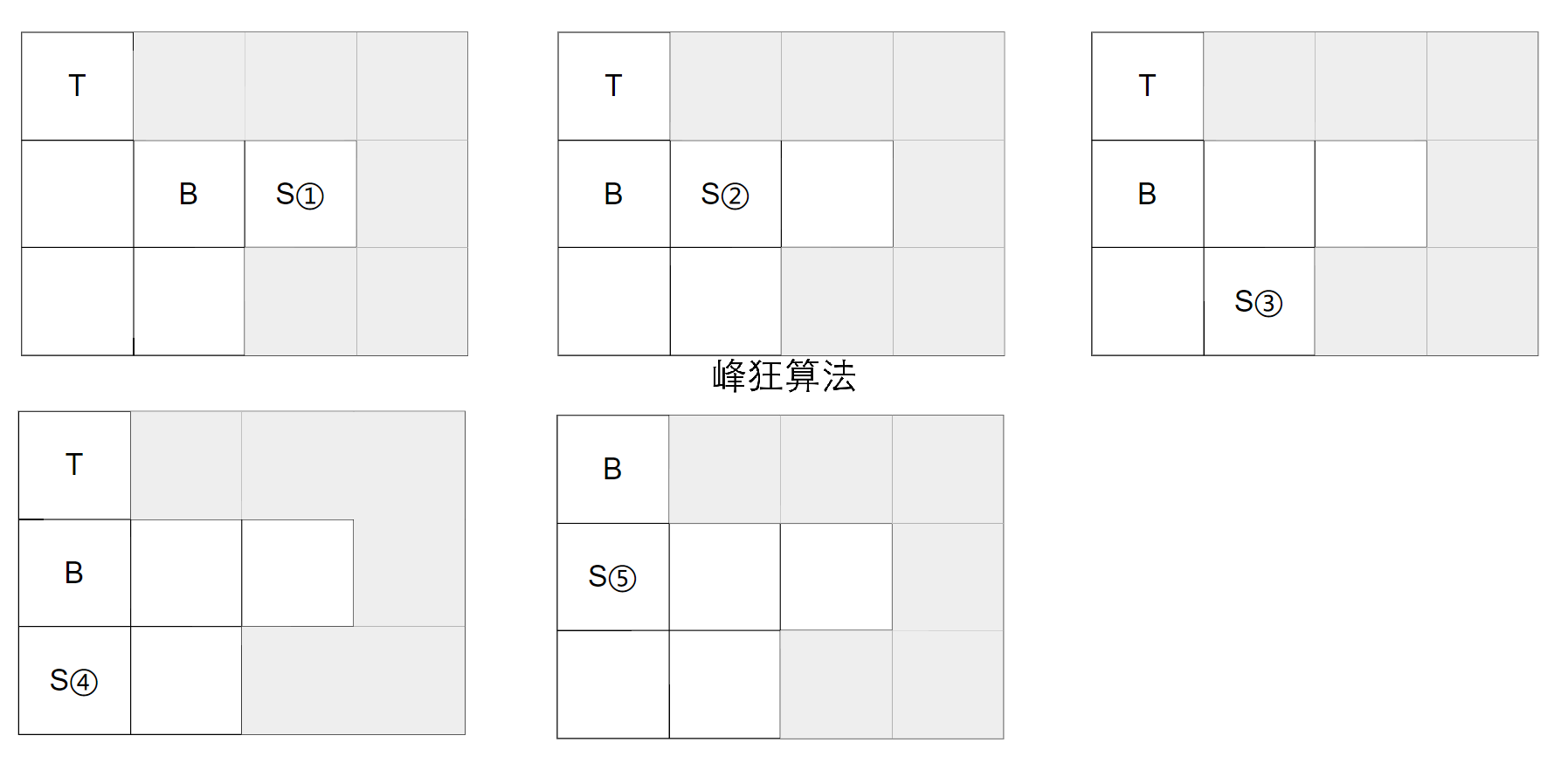
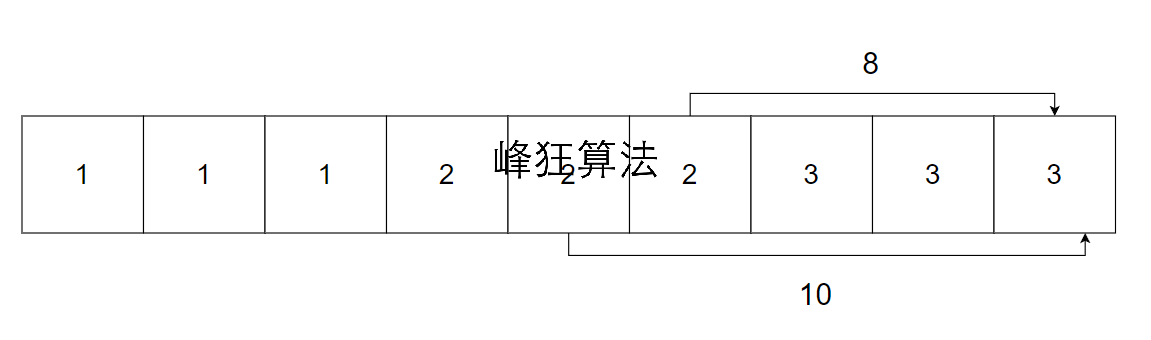
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
#include <bits/stdc++.h>
using namespace std;
const int maxn = 25, inf = 0x3f3f3f3f;
char s[maxn][maxn];
// 0 ~ 3上下左右
const int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1};
// 箱子、人的上下左右字母
const char A[4] = {'N', 'S', 'W', 'E'}, a[4] = {'n', 's', 'w', 'e'};
int r, c;
string path;

struct node {
  // b代表box箱子，p代表person人
  int bx_, by_, px_, py_;
  // 经过的路径
  string path_;
} bg;

// 初始化起点
void init() {
  for (int i = 1; i <= r; ++i) {
    for (int j = 1; j <= c; ++j) {
      if (s[i][j] == 'B') {
        bg.bx_ = i, bg.by_ = j, s[i][j] = '.';
      } else if (s[i][j] == 'S') {
        bg.px_ = i, bg.py_ = j, s[i][j] = '.';
      }
    }
  }
}

bool valid(int x, int y) {
  return x >= 1 && y >= 1 && x <= r && y <= c && s[x][y] != '#';
}

int calc(string &str) {
  int res = 0;
  for (int i = 0; i < str.length(); ++i) {
    if (isupper(str[i])) ++res;
  }
  return res;
}

bool bfs2(node from, node to) {
  queue<node> q;
  bool vis[maxn][maxn];
  memset(vis, 0, sizeof(vis));
  // 不可能从箱子上碾过去
  vis[from.bx_][from.by_] = 1;
  q.push(from);
  while (!q.empty()) {
    node u = q.front();
    q.pop();
    if (u.px_ == to.px_ && u.py_ == to.py_) {
      path = u.path_;
      return 1;
    }
    for (int i = 0; i < 4; ++i) {
      int x = u.px_ + dx[i], y = u.py_ + dy[i];
      if (!valid(x, y)) continue;
      if (vis[x][y]) continue;
      node nxt;
      nxt.px_ = x, nxt.py_ = y, nxt.path_ = u.path_ + a[i];
      vis[x][y] = 1;
      q.push(nxt);
    }
  }
  return 0;
}

string bfs1() {
  init();
  queue<node> q;
  string ans = "Impossible.";
  // 总路径最小值，箱子路径最小值
  // 若直接保存人的路径最小值，两变量相互独立，无法保证箱子路径最小这一前提
  int path_len = inf, box_len = inf;
  // 当前状态下，箱子和人的路径最小值
  int box[maxn][maxn][4], people[maxn][maxn][4];
  memset(box, 0x3f, sizeof(box)), memset(people, 0x3f, sizeof(people));
  q.push(bg);
  while (!q.empty()) {
    node u = q.front();
    q.pop();
    if (s[u.bx_][u.by_] == 'T') {
      int pl = u.path_.length(), bl = calc(u.path_);
      // 先保证箱子路径最小，再保证人路径最小
      if (bl < box_len || (bl == box_len && pl < path_len)) {
        ans = u.path_, path_len = pl, box_len = bl;
      }
      continue;
    }
    for (int i = 0; i < 4; ++i) {
      int x = u.bx_ + dx[i], y = u.by_ + dy[i];
      if (!valid(x, y)) continue;
      // 人应该从people_from跑到people_to的位置才能推箱子
      node people_from = u, people_to;
      people_from.path_ = "";
      if (i == 0) {
        people_to.px_ = u.bx_ + 1, people_to.py_ = u.by_;
      } else if (i == 1) {
        people_to.px_ = u.bx_ - 1, people_to.py_ = u.by_;
      } else if (i == 2) {
        people_to.py_ = u.by_ + 1, people_to.px_ = u.bx_;
      } else {
        people_to.py_ = u.by_ - 1, people_to.px_ = u.bx_;
      }
      if (!valid(people_to.px_, people_to.py_)) continue;
      if (!bfs2(people_from, people_to)) continue;
      node nxt;
      nxt.bx_ = x, nxt.by_ = y, nxt.px_ = u.bx_, nxt.py_ = u.by_;
      nxt.path_ = u.path_ + path + A[i];
      // SPFA收敛性判断
      int bl = calc(nxt.path_), pl = nxt.path_.length() - bl;
      if (box[u.bx_][u.by_][i] < bl || people[u.bx_][u.by_][i] < pl) continue;
      box[u.bx_][u.by_][i] = bl, people[u.bx_][u.by_][i] = pl;
      q.push(nxt);
    }
  }
  return ans;
}

int main() {
  int num = 0;
  while (cin >> r >> c && r && c) {
    for (int i = 1; i <= r; ++i) cin >> (s[i] + 1);
    cout << "Maze #" << ++num << endl << bfs1() << endl << endl;
  }
  return 0;
}

思路

双重BFS的经典例题，也是dijkstra和spfa的精髓题，直接上图。

移动方式如下图所示：

本题最大的难点在于，对dijkstra和spfa算法的理解，否则压根看不懂题解。

题目要求先保证箱子的路径最短，再保证人的路径最短。

人走到箱子旁边这一部分，正常编写BFS是没错的，

因为BFS本质是对一张边权均为1的图作dijkstra，所以第一次遇到终止态时就是答案（显然）；

但箱子的移动部分，你必须采用spfa算法：

  1. 对箱子进行普通BFS确实没错，对箱子的角度而言；其下一步的路径数肯定是不小于上一步的，是线性不减；

    但是你能保证人的路径数也线性不减吗？尽管人是跟着箱子动的，但是人的位置是随机变化的啊！

  2. 所以正确的做法是，利用spfa的思维，单独开box[x][y][dir]和people[x][y][dir]数组，

    分别记录(x,y,dir)状态下箱子的最短路径和人的最短路径，只要有一者会更小，就继续BFS，直到收敛。