考点
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 50;
ll n1, n2, m, ans[maxn], f[maxn][20];
struct node {
ll id_, c_, d_;
bool operator<(node &b) { return c_ < b.c_ || (c_ == b.c_ && d_ < b.d_); }
} s[2 * maxn];
void init() {
for (int i = 1; i <= n1; ++i) {
if (s[i].d_ < s[i].c_) s[i].d_ += m;
s[i + n1] = s[i], s[i + n1].c_ += m, s[i + n1].d_ += m;
}
n2 = n1 * 2;
sort(s + 1, s + 1 + n2);
for (int i = 1, j = 1; i <= n2; ++i) {
while (j <= n2 && s[j].c_ <= s[i].d_) ++j;
f[i][0] = j - 1;
}
for (int j = 1; (1 << j) <= n1; ++j) {
for (int i = 1; i <= n2; ++i) {
f[i][j] = f[f[i][j - 1]][j - 1];
}
}
}
void work(int x) {
ll bg = x, ed = s[x].c_ + m, cnt = 1, nxt;
for (int i = 19; i >= 0; --i) {
nxt = f[x][i];
if (nxt && s[nxt].d_ < ed) {
x = f[x][i];
cnt += (1 << i);
}
}
ans[s[bg].id_] = cnt + 1;
}
int main() {
cin >> n1 >> m;
for (int i = 1; i <= n1; ++i) cin >> s[i].c_ >> s[i].d_, s[i].id_ = i;
init();
for (int i = 1; i <= n1; ++i) work(i);
for (int i = 1; i <= n1; ++i) cout << ans[i] << " ";
return 0;
}
|
思路
断环为链+左端点排序后,变成如下模样:
假设从2出发,题目是问你到达2 + 8 = 10最少需要几个人,
即第二圈(断环为链的美妙)
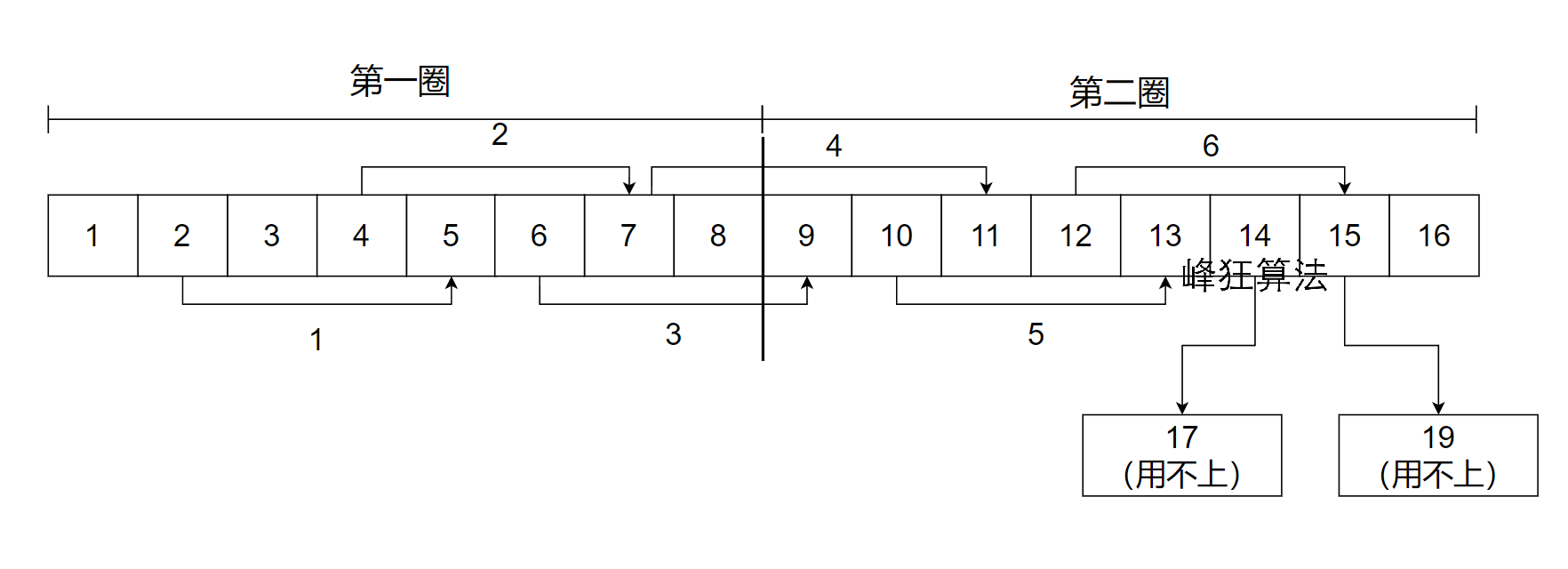
题目已经说了,跳跃区间彼此不会包含;
通过对链的左端点排序之后,沿着跳跃区间走,只会前进不会回头,很重要的单调性!
由于题目要寻找最少的人数,每个战士应该把接力棒交给离他尽可能远、但在当前范围内的人,即最远下一跳;
所以利用上述单调性,直接用双指针线性时间复杂度就能处理好,如图所示:
a的最远下一跳是c,显然b的最远下一跳至少是c;所以不可能回头,可以用双指针
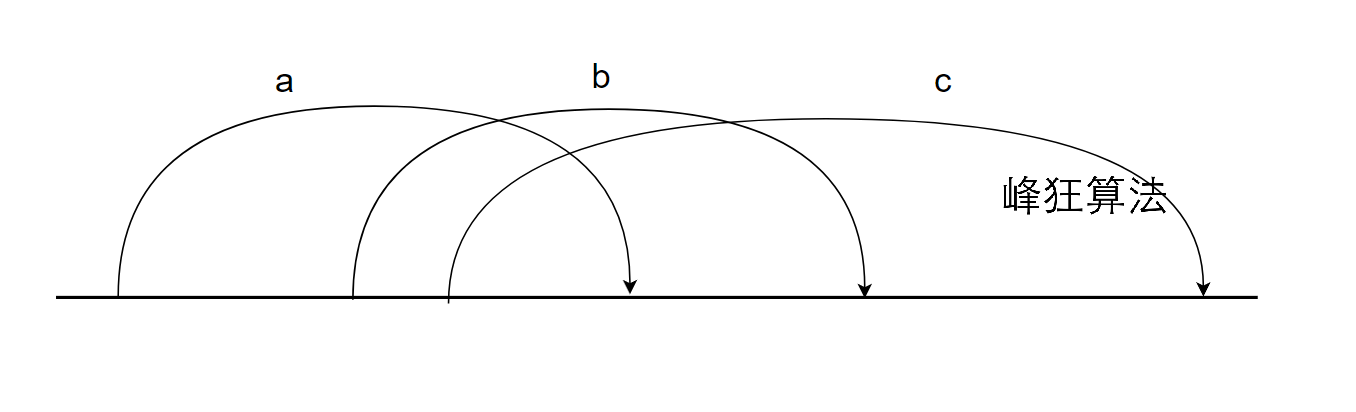
跳跃过程结合上述每个人的最远下一跳,直接套倍增板子即可~
最后一个难点,我跳过终点也算第二圈,刚好跳到终点同样算第二圈,怎么计数?
最终答案 = 尽可能逼近终点(不是等于,也不是大于,是小于!)所需的最少人数 + 1
因为题目说过数据保证整个边境线都是可被覆盖的,去掉等于或大于终点的最后一人,那之前所有人不都在终点以内吗?
正难则反哟!

