P6648. Triangle The Data Structure

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 696 阅读时长 ≈ 2 分钟

考点

  • st表
  • 单调队列

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 3e3 + 50;
int n, K, lg, head, tail, q[maxn], st[maxn][maxn];

void init() {
  for (int k = 1; k <= lg; ++k) {
    int r = n - (1 << k) + 1, v = 1 << (k - 1);
    for (int i = 1; i <= r; ++i) {
      head = tail = 0;
      for (int j = 1; j <= v; ++j) {
        while (head < tail && st[i + v][j] >= st[i + v][q[tail - 1]]) --tail;
        q[tail++] = j;
      }
      for (int j = 1; j <= i; ++j) {
        while (head < tail && j + v - q[head] > v) ++head;
        while (head < tail && st[i + v][j + v] >= st[i + v][q[tail - 1]])
          --tail;
        q[tail++] = j + v;
        st[i][j] = max(st[i][j], st[i + v][q[head]]);
      }
    }
  }
}

ll work() {
  ll ans = 0;
  int r = n - K + 1;
  for (int i = 1; i <= r; ++i) {
    head = tail = 0;
    int cnt = i + K - (1 << lg), v = cnt - i;
    for (int j = 1; j <= v; ++j) {
      while (head < tail && st[cnt][j] >= st[cnt][q[tail - 1]]) --tail;
      q[tail++] = j;
    }
    for (int j = 1; j <= i; ++j) {
      while (head < tail && j + v - q[head] > v) ++head;
      while (head < tail && st[cnt][j + v] >= st[cnt][q[tail - 1]]) --tail;
      q[tail++] = j + v;
      ans += max(st[i][j], st[cnt][q[head]]);
    }
  }
  return ans;
}

int main() {
  cin >> n >> K;
  lg = log2(K);
  for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= i; ++j) {
      cin >> st[i][j];
    }
  }
  init();
  cout << work();
  return 0;
}

思路

考虑类似ST表的做法。

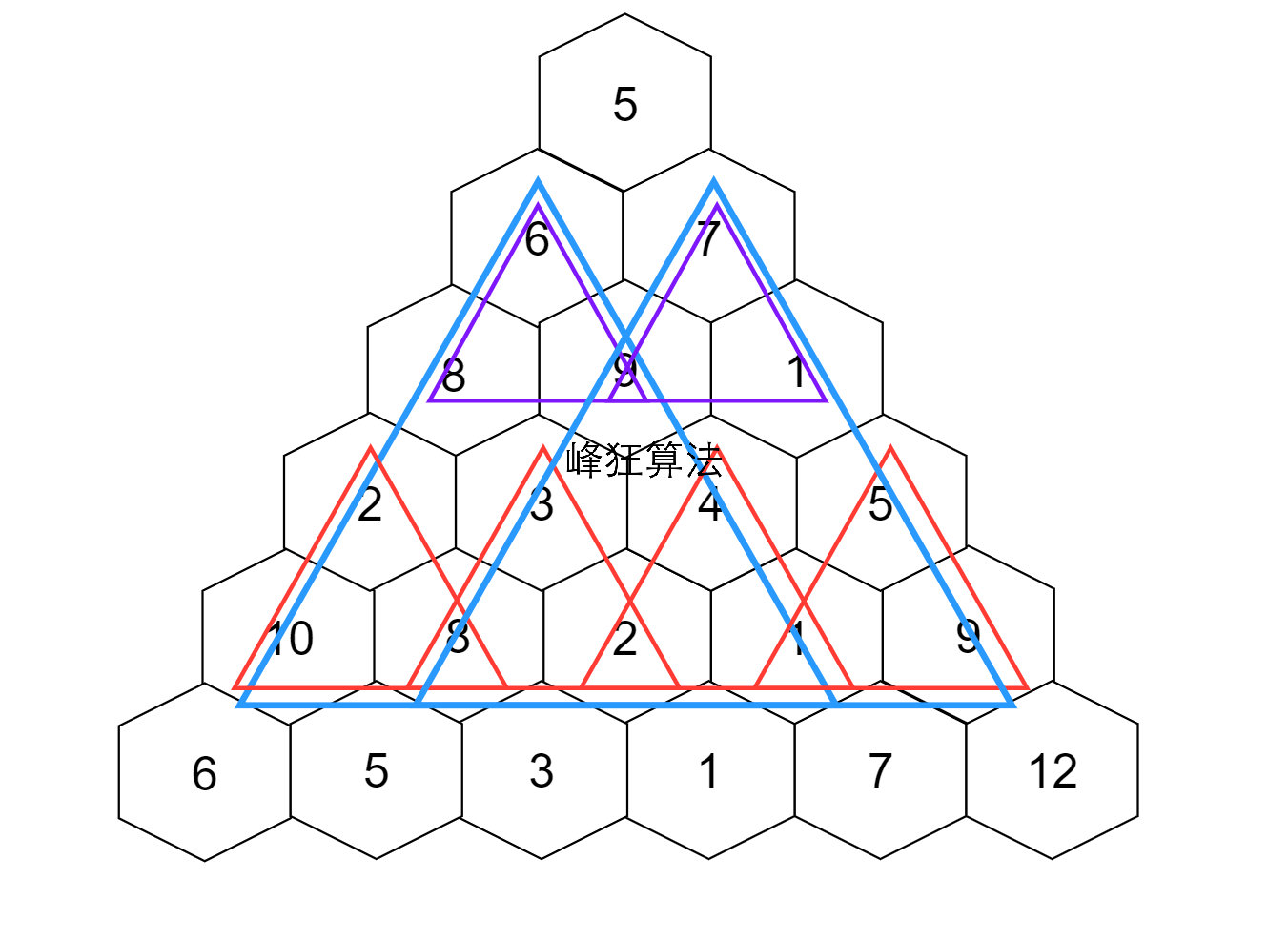
令st[i][j][k]代表以(i, j)为顶点，边长为2k的正三角形的最大值，可以得到： \[ st\left[ i \right] \left[ j \right] \left[ k \right] =\max \left( \begin{matrix} st\left[ i \right] \left[ j \right] \left[ k-1 \right] ,& \max \begin{array}{c} j+2^{k-1}\\ t=j\\ \end{array}st\left[ i+2^{k-1} \right] \left[ t \right] \left[ k-1 \right]\\ \end{matrix} \right) \] 可能文字有点抽象，我画个图：

每个大的、边长为4的蓝色三角形，由一个边长为2的紫色三角形和若干个边长为2的红色三角形组成。

假设当前大蓝色三角形顶点为(i, j)，长度为2k，可以发现以下规律：

  • 只有一个顶点为(i, j)，长度为2k-1的紫色三角形

  • 从第i + 2k-1行、第j列开始，有连续2k-1 + 1个，长度为2k-1的红色三角形

    是1 + 2k-1个！

  • 第i行有i个点

根据上述规则进行编程，可以发现几个优化点：

  • st表数组的第三维可以用滚动数组的思想去掉，毕竟只需要上一次的数据

  • 幂次枚举到log2(k)即可

  • 求每个蓝色三角形中红色三角形们的极值，可以用单调队列进行优化

    从图上可以显然发现，红色三角形们都是挨着的——

    所以可以先填充2k-1个红色三角形到单调队列中，然后每右移1个红色三角形，蓝色三角形顶点也右移1个

    即可达到线性同步更新的骚操作~