考点
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 50;
ll n, k, m, a[maxn], nxt[maxn], fa[maxn][62];
void init() {
int l = 1, r = 1 + k;
for (int i = 1; i <= n; ++i) {
while (r + 1 <= n && a[r + 1] - a[i] < a[i] - a[l]) ++l, ++r;
nxt[i] = a[r] - a[i] > a[i] - a[l] ? r : l;
}
for (int i = 1; i <= n; ++i) fa[i][0] = nxt[i];
for (int j = 1; j <= 61; ++j) {
for (int i = 1; i <= n; ++i) {
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
}
}
int jump(int bg, ll x) {
for (int i = 61; i >= 0; --i) {
if (x >= (1ll << i)) {
bg = fa[bg][i];
x -= (1ll << i);
}
}
return bg;
}
int main() {
cin >> n >> k >> m;
for (int i = 1; i <= n; ++i) cin >> a[i];
init();
for (int i = 1; i <= n; ++i) cout << jump(i, m) << " ";
return 0;
}
|
思路
最大的难点在于计算每个元素的第k远。
其实翻译的语义是有问题的,英文原话明明是叫你找第K小.....
假设对于点A有距离数组{5, 4, 3, A, 1, 2, 8},
第1小跳到元素1,第2小跳到元素2,第3小跳到元素3,第4小跳到元素4,第5小元素5,第6小元素8
以当前元素A做距离数组,用双指针维护一个长度为k + 1的滑动窗口,
在滑动窗口中,A的左边称之为左半部分,A的右边称之为右半部分,移动流程如下:

最后比较左、右两部分谁的最大值更大即可。
还有一个难点,为什么可以用滑动窗口,前一个元素不会影响后一个元素的结果吗?
那就证明一下:
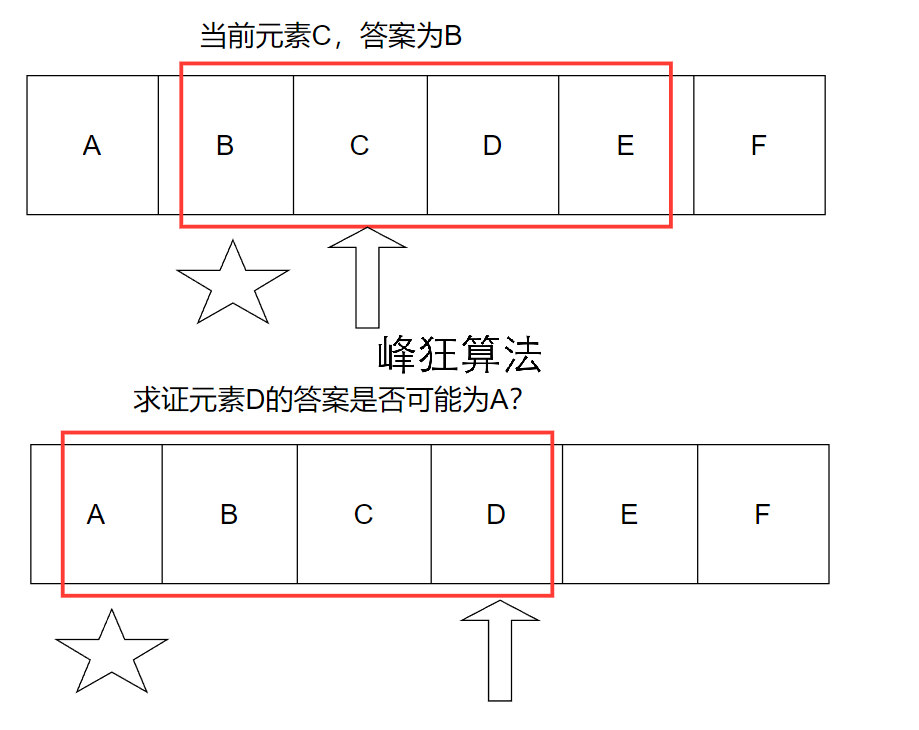
假设D的答案是A,那么\(\left| ED
\right|>\left| AD \right|\)
又因为已知元素C的答案为B,那么\(\left| AC
\right|>\left| EC \right|\),一定有\(\left| AD \right|>\left| ED
\right|\)
两者相悖,反证法毕。
后续直接用倍增优化跳链即可,不再赘述。

