考点
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 50;
int n, q, f[maxn][20], g[maxn][20];
int st[maxn], top;
struct node {
int d_, v_, nxt_;
} a[maxn];
int main() {
cin >> n >> q;
for (int i = 1; i <= n; ++i) cin >> a[i].d_ >> a[i].v_;
++n;
a[n].d_ = a[n].v_ = 0x3f3f3f3f;
for (int i = 1; i <= n; ++i) {
while (top > 0 && a[i].d_ > a[st[top]].d_) a[st[top--]].nxt_ = i;
st[++top] = i;
}
while (top > 0) a[st[top--]].nxt_ = n;
for (int i = 1; i < n; ++i) f[i][0] = a[i].nxt_, g[i][0] = a[i].v_;
for (int j = 1; j <= 18; ++j) {
for (int i = 1; i < n; ++i) {
f[i][j] = f[f[i][j - 1]][j - 1];
g[i][j] = g[i][j - 1] + g[f[i][j - 1]][j - 1];
}
}
int r, v;
while (q--) {
cin >> r >> v;
for (int i = 18; i >= 0; --i) {
if (v > g[r][i]) {
v -= g[r][i];
r = f[r][i];
}
}
cout << (r == n ? 0 : r) << endl;
}
return 0;
}
|
思路
把盘子们倒过来看,俨然是一个结构体数组:
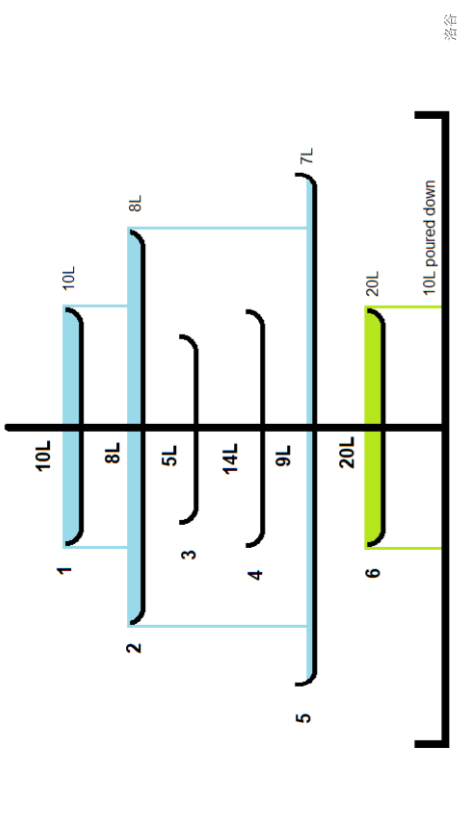
设盘子结构体如下,设水池也为一个直径无穷大、容积无穷大的盘子:
1
2
3
| struct node {
int d_, v_, nxt_;
}
|
d代表直径,v代表容积,nxt代表右侧第一个大于d的盘子。
每个盘子都要向右找第一个大于自己d的盘子(除了水池),维护一个单调不增(单调递减or相等)的单调栈即可。
普通情况下,每次询问都一层层跑nxt,整个过程就是链式的\(O(n)\)复杂度,肯定TLE。
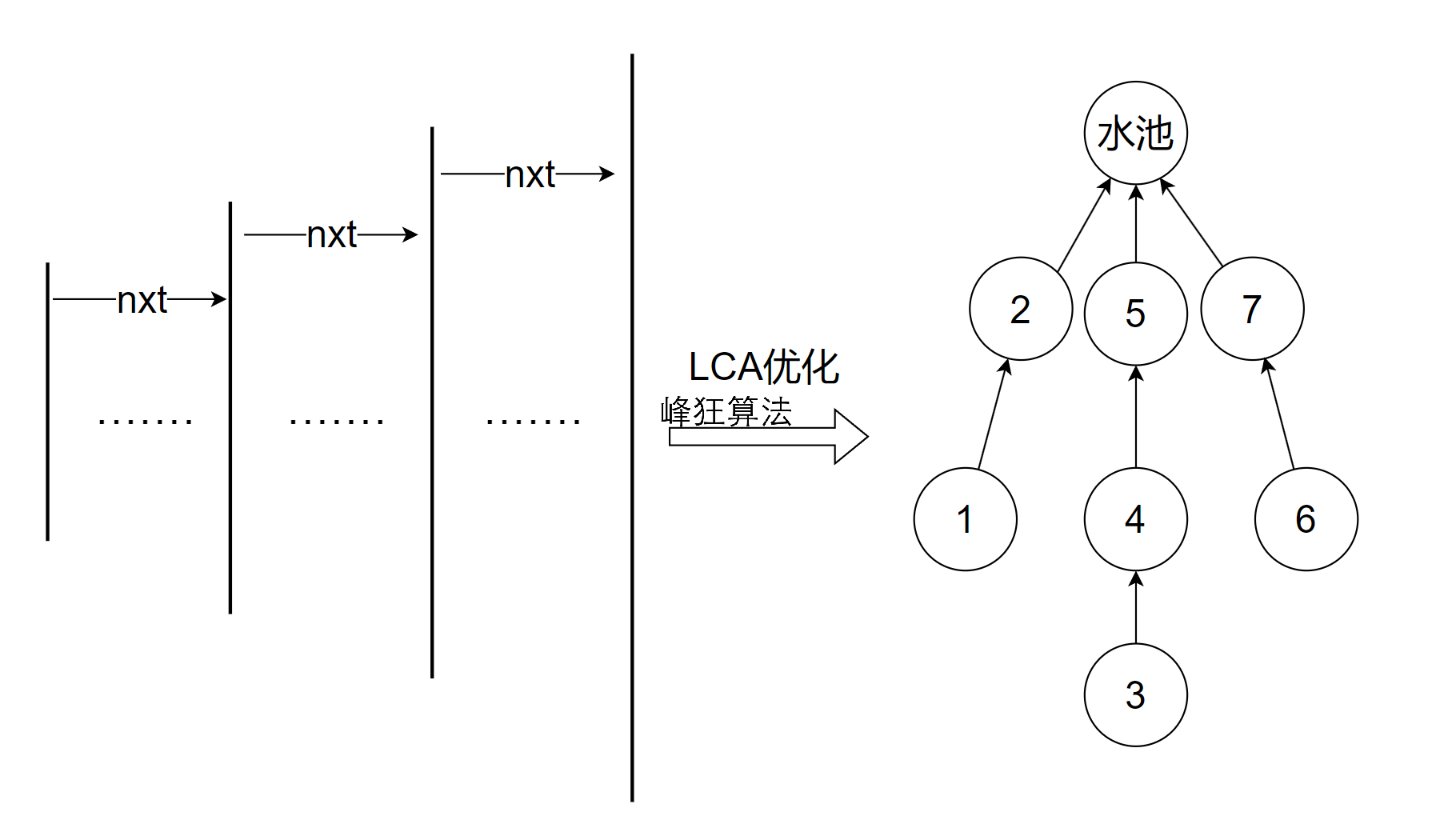
用LCA的倍增实现跳链,那么水池就是根结点,每个结点的nxt序列抽象为树的路径:
令f[i][j]为盘子i跳2j个盘子后到达的盘子,有f[i][j] = f[f[i][j-1]][j-1]
显然初始时f[i][0] = 盘子i的nxt
令g[i][j]为盘子i跳到f[i][j]所需要的容积,有g[i][j] = g[i][j - 1] + g[f[i][j - 1]][j - 1]
显然初始时g[i][0] = 盘子i的v,至少大于当前盘子的容积才能流到下个盘子不是吗?

