P1908. 逆序对

发表于 分类于 阅读次数： Waline： 本文字数： 484 阅读时长 ≈ 2 分钟

考点

  • 排序
  • 树状数组

题解

见思路

思路

归并排序

考虑归并排序时的合并操作，以下图为例，游标j的移动范围为1~4，游标k的移动范围为5~8

左边界l为下标1，右边界r为下标8

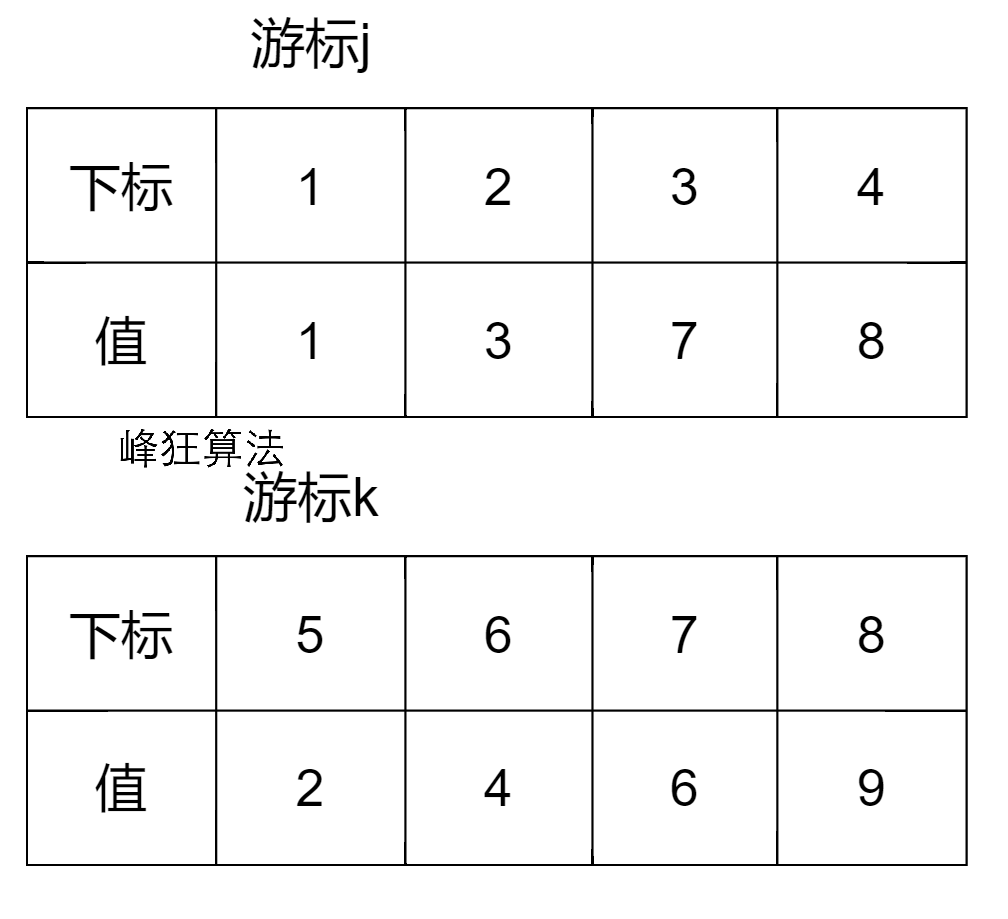
第一轮：j = 1，k = 5，a[j] = 1 < a[k] = 2且j < k，a[j]纳入答案且j++

第二轮：j = 2，k = 5，a[j] = 3 > a[k] = 2且j < k，a[k]纳入答案且k++

注意！这里出现了3个逆序对，a[5]小于{a[2]，a[3]，a[4]}，但下标却大于它们。

这样就能得到逆序对的公式：((l + r) / 2) - j + 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 50;
int n, a[maxn], t[maxn];
ll ans = 0;

void merge(int l, int r) {
  if (l == r) return;
  int i = l, j = l, mid = (l + r) / 2, k = mid + 1;
  merge(l, mid), merge(mid + 1, r);
  while (j <= mid && k <= r) {
    if (a[j] <= a[k]) {
      t[i++] = a[j++];
    } else {
      t[i++] = a[k++];
      ans += mid - j + 1;
    }
  }
  while (j <= mid) t[i++] = a[j++];
  while (k <= r) t[i++] = a[k++];
  for (i = l; i <= r; ++i) a[i] = t[i];
}

int main() {
  cin >> n;
  for (int i = 1; i <= n; ++i) cin >> a[i];
  merge(1, n);
  cout << ans;
  return 0;
}

权值树状数组

先离散化，得知每个元素的排名；

倒序遍历数组，统计比当前元素排名小的个数，即为逆序对；然后再把该元素添加进树状数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 50;
ll n, ans, dtot, a[maxn], bit[maxn], dis[maxn];

int lowbit(int x) { return x & -x; }

void add(int x, int v) {
  while (x <= n) {
    bit[x] += v;
    x += lowbit(x);
  }
}

ll query(int x) {
  ll res = 0;
  while (x > 0) {
    res += bit[x];
    x -= lowbit(x);
  }
  return res;
}

int main() {
  cin >> n;
  for (int i = 1; i <= n; ++i) cin >> a[i], dis[++dtot] = a[i];
  sort(dis + 1, dis + 1 + dtot);
  dtot = unique(dis + 1, dis + 1 + dtot) - 1 - dis;
  ll res = 0;
  for (int rk, i = n; i >= 1; --i) {
    rk = lower_bound(dis + 1, dis + 1 + dtot, a[i]) - dis;
    res += query(rk - 1);
    add(rk, 1);
  }
  cout << res;
  return 0;
}