P2882. Face The Right Way G

发表于 分类于 阅读次数： Waline： 本文字数： 493 阅读时长 ≈ 2 分钟

考点

  • 贪心
  • 差分

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e3 + 50;
int n, K, M, diff[maxn];
char a[maxn];

int main() {
  cin >> n;
  K = M = INT_MAX;
  for (int i = 1; i <= n; ++i) cin >> a[i];
  for (int k = 1; k <= n; ++k) {
    int m = 0;
    bool flag = true;
    memset(diff, 0, sizeof(diff));
    for (int i = 1; i <= n; ++i) {
      diff[i] ^= diff[i - 1];
      if (a[i] == 'F' && diff[i] || a[i] == 'B' && !diff[i]) {
        if (i + k - 1 <= n) {
          ++m;
          diff[i + 1] ^= 1, diff[i + k] ^= 1;
        } else {
          flag = false;
          break;
        }
      }
    }
    if (flag && m < M) K = k, M = m;
  }
  cout << K << " " << M;
  return 0;
}

思路

在固定k的情况下，如何让m最小呢？先翻转B个数多的那一段k吗？万一每段k的B个数相同该怎么办？

贪心的侧重点不在增加k中 B的个数，而是尽可能减少修改k中的F；

白话文就是，尽可能减少拆东墙（改变F）补西墙（改变B）的次数。

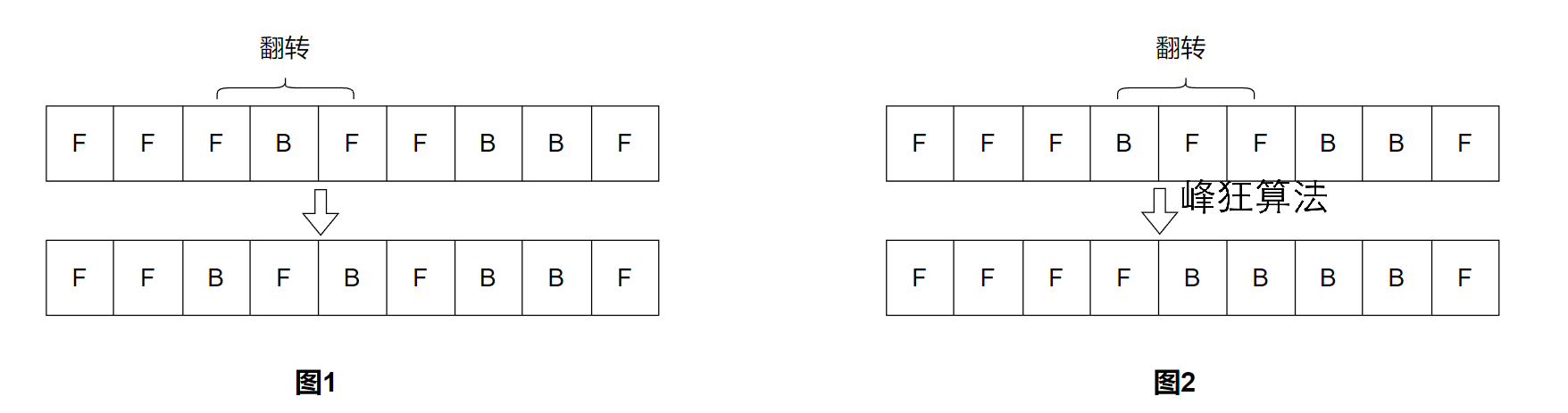
如下图所示，范围[1, 3]内都是连续的F，图2显然比图1更优：

  • 图1拆了[1, 3]内的一个F，且不管后续如何，对于[1, 3]而言这就是劣的
  • 图2没拆[1, 3]，且不管后续如何，对于[1, 3]而言这就是优的

制定最终的贪心思路：

  • 尝试维护一个[1, n]的最长连续F序列，遍历顺序应该是从左到右或从右到左；

    这里选择从左到右。

  • 假设当前下标为x，[1, x - 1]已经是连续的F序列，不能回头动这个区间；

    那么只要当前为B，就向右修改[x, x + k - 1]。

  • 如果最后[n - k + 2, n]区间内还有B，说明贪心失败；反之成功。

修改区间可以用双指针，但是时间复杂度为平方级，用差分进行优化。

最后一个问题，枚举k可以用二分优化吗？

显然不可以，k小难道m就小了吗？k大难道m就大了吗？

只能暴力枚举啦~