考点
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 5e2 + 50;
int R, C, A, B, pre[maxn][maxn];
int query(int x1, int y1, int x2, int y2) {
return pre[x2][y2] - pre[x1 - 1][y2] - pre[x2][y1 - 1] + pre[x1 - 1][y1 - 1];
}
bool check(int s) {
int valid = 0, x1 = 1, y1 = 1, x2 = 1, y2 = 1;
while (x1 <= R && x2 <= R) {
int block = 0;
while (y2 <= C) {
if (query(x1, y1, x2, y2) >= s) {
++block;
y1 = y2 + 1;
}
++y2;
}
if (block >= B) {
++valid;
x2 = x1 = x2 + 1;
} else {
++x2;
}
y1 = y2 = 1;
}
return valid >= A;
}
int main() {
cin >> R >> C >> A >> B;
for (int i = 1; i <= R; ++i) {
for (int j = 1; j <= C; ++j) {
cin >> pre[i][j];
pre[i][j] += pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1];
}
}
int l = 0, r = pre[R][C];
while (l <= r) {
int mid = l + (r - l) / 2;
if (check(mid)) {
l = mid + 1;
} else {
r = mid - 1;
}
}
cout << r;
return 0;
}
|
思路
由于横切和竖切组合有接近无数种切法,靠暴力枚举找答案是绝对行不通的。
题目要让最小值最大,考虑二分答案:
令s为所有蛋糕块里的最小值,
如果s是合法的,那么所有蛋糕块均为s的情况下,得到的块数一定是大于等于A * B的。
由此可以得到单调性:
s越大,总块数越小于A * Bs越小,总块数越大于A * B- 若总块数大于等于
A * B,说明s过小了,应该增大
- 若总块数小于
A * B,说明s过大了,应该减小
由于轮询的都是二维区间和,须用二维前缀和进行优化。
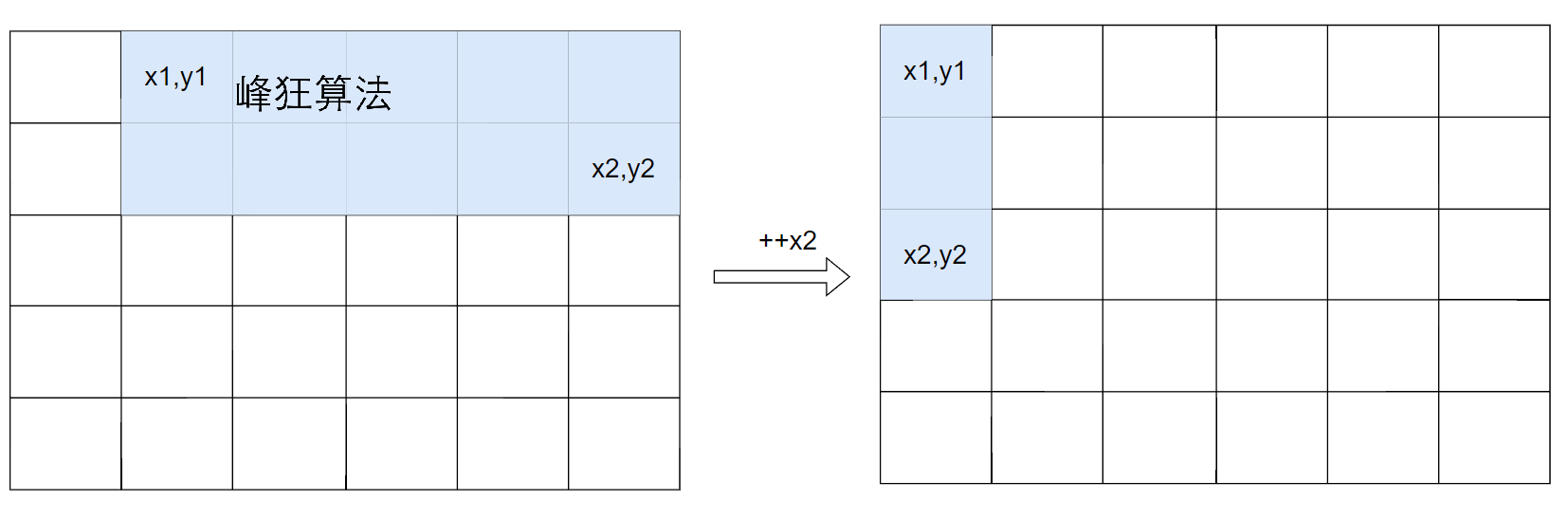
设(x1,y1)为矩形左上角,(x2,y2)为矩形右下角
每次移动y2并判定矩形的和是否达到s,若是的话则令y1 = y2 + 1,进入下一次竖切:
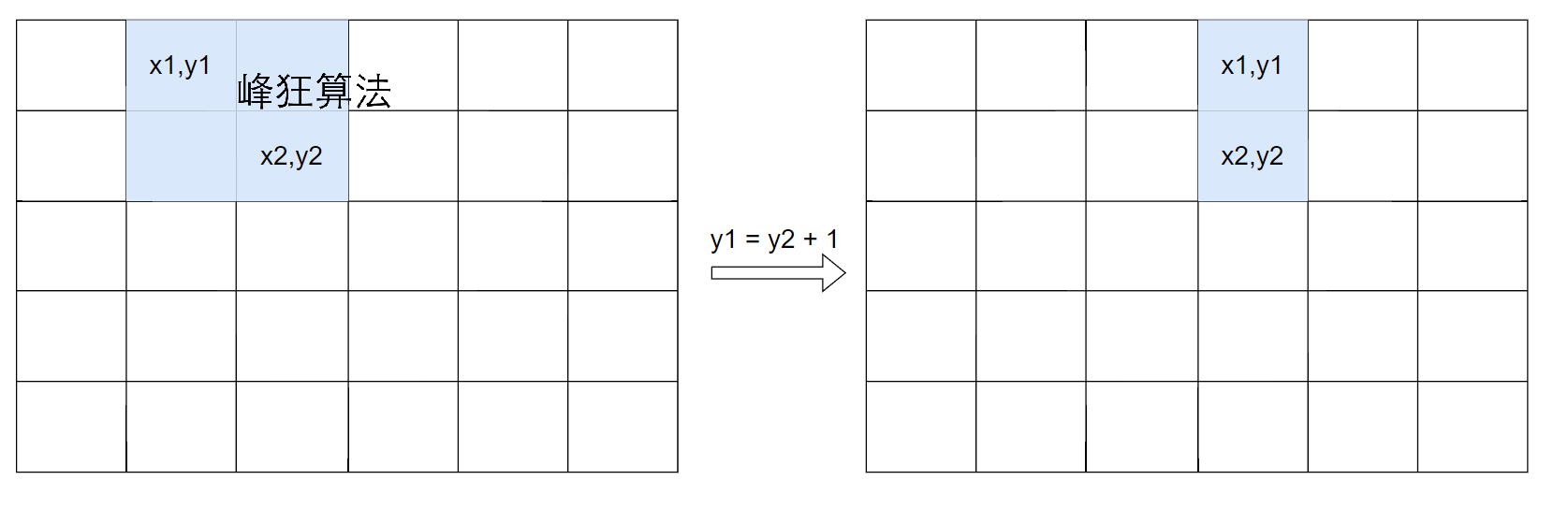
当y2 == C时,即本轮竖切全部结束后进行判定,随后令y1 = y2 = 1进行复位:
如果块数大于等于B,可进入下一次横切。
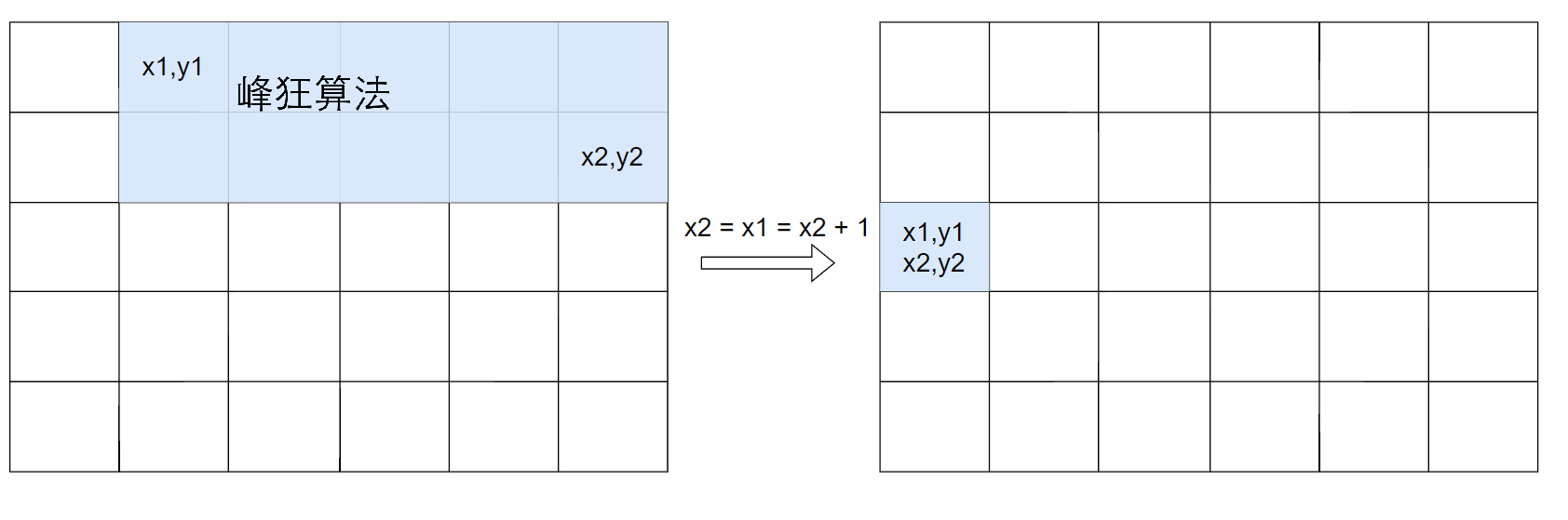
如果块数小于B,和下一行合并后,再次竖切。