P4653. Sure Bet

发表于 分类于 阅读次数： Waline： 本文字数： 377 阅读时长 ≈ 1 分钟

考点

  • 双指针
  • 前缀和

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 50;
int n;
double ans, lsum, rsum, a[maxn], b[maxn];

bool cmp(double &x, double &y) { return x > y; }

int main() {
  cin >> n;
  for (int i = 1; i <= n; ++i) cin >> a[i] >> b[i];
  sort(a + 1, a + 1 + n, cmp), sort(b + 1, b + 1 + n, cmp);
  int l = 1, r = 1;
  while (l <= n && r <= n) {
    while (l <= n && lsum <= rsum) {
      //r - 1是因为此刻l可取，但r不可取
      lsum += a[l], ans = max(ans, min(lsum, rsum) - (l + r - 1)), ++l;
    }
    while (r <= n && rsum < lsum) {
      //l - 1是因为此刻r可取，但l不可取
      rsum += b[r], ans = max(ans, min(lsum, rsum) - (l - 1 + r)), ++r;
    }
  }
  cout << fixed << setprecision(4) << ans;
  return 0;
}

思路

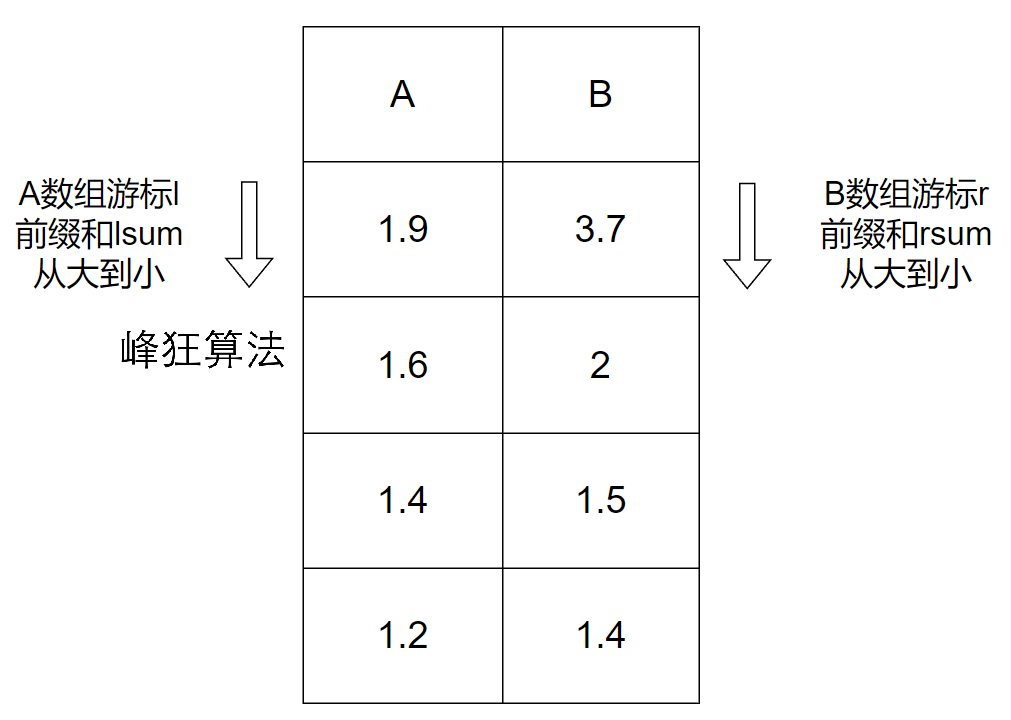
A与B数组各取任意数量元素（代表顺序无关）；设A数组取l个，其和为lsum；设B数组取r个，其和为rsum；

题目要让min(lsum, rsum) - (l + r)最大。

两数组各自从大到小排序后，可直接套用贪心，因为很显然：

l和r都在增加，必须也要让min(lsum, rsum)尽可能大；

由于是从大到小排序，显然在相同长度的情况下，A或B数组的前缀和是最大的；

所以l可直接等价为A数组游标，r可直接等价为B数组游标；

lsum可直接等价为A数组的前缀和，rsum可直接等价为B数组的前缀和；

每次只需要判断lsum和rsum谁更小，谁的游标就新增一个（因为要让最小值最大，维持平衡）