P1950. 长方形
考点
- 单调栈
- 悬线法
题解
1 |
|
思路
本题是P4147的升级版,请先掌握该题;题目问有多少种剪矩形的办法。
根据悬线法可知,一个最大矩形可以由中线切开,组成的可能性 = 左半部分的可能性 * 右半部分的可能性
本题实际上就是求每个悬线向左和向右的最大扩展距离罢了~
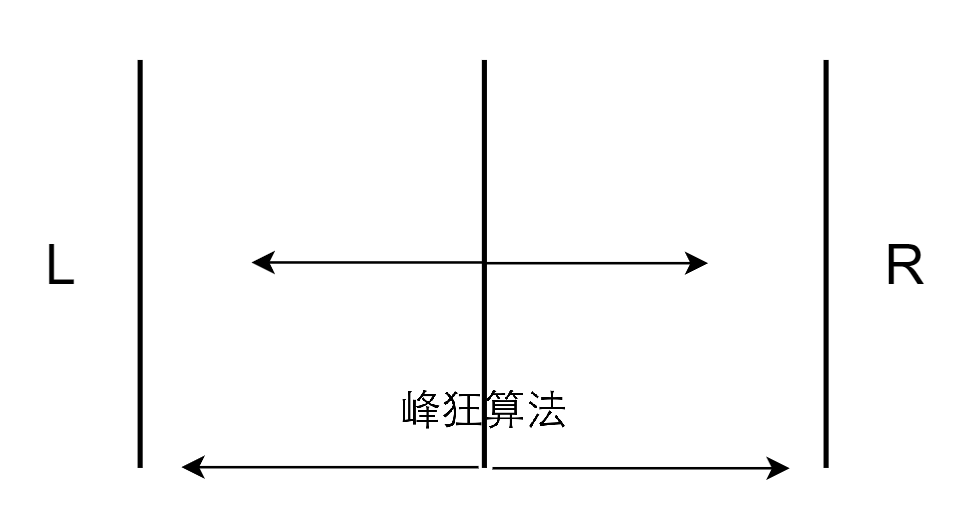
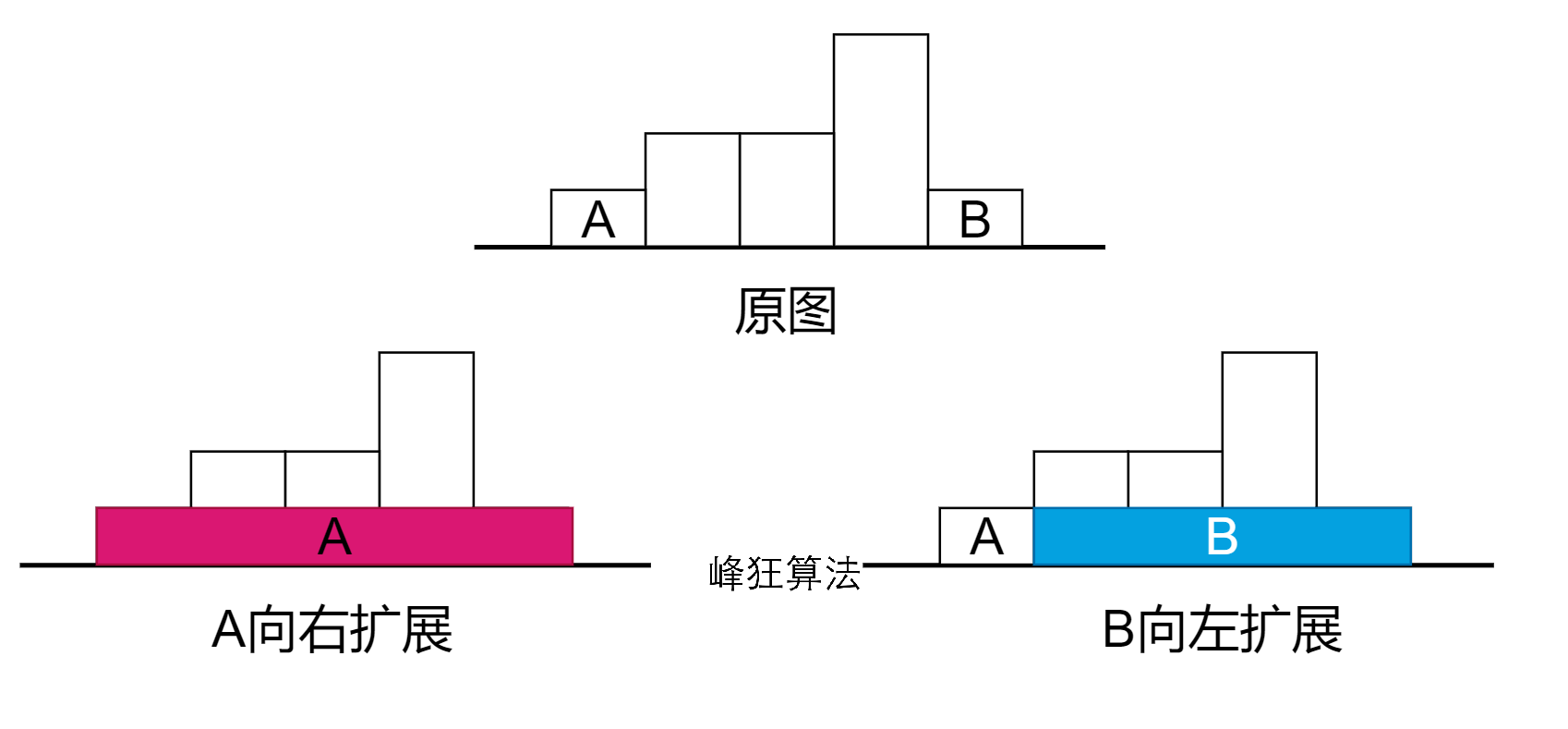
但是要注意不重不漏哟,如下图所示:
A向右扩展时可以和P4147一样正常找最大
B向左扩展时遇到高度小于等于时就终止,因为A向右扩展时已经找过最大值了
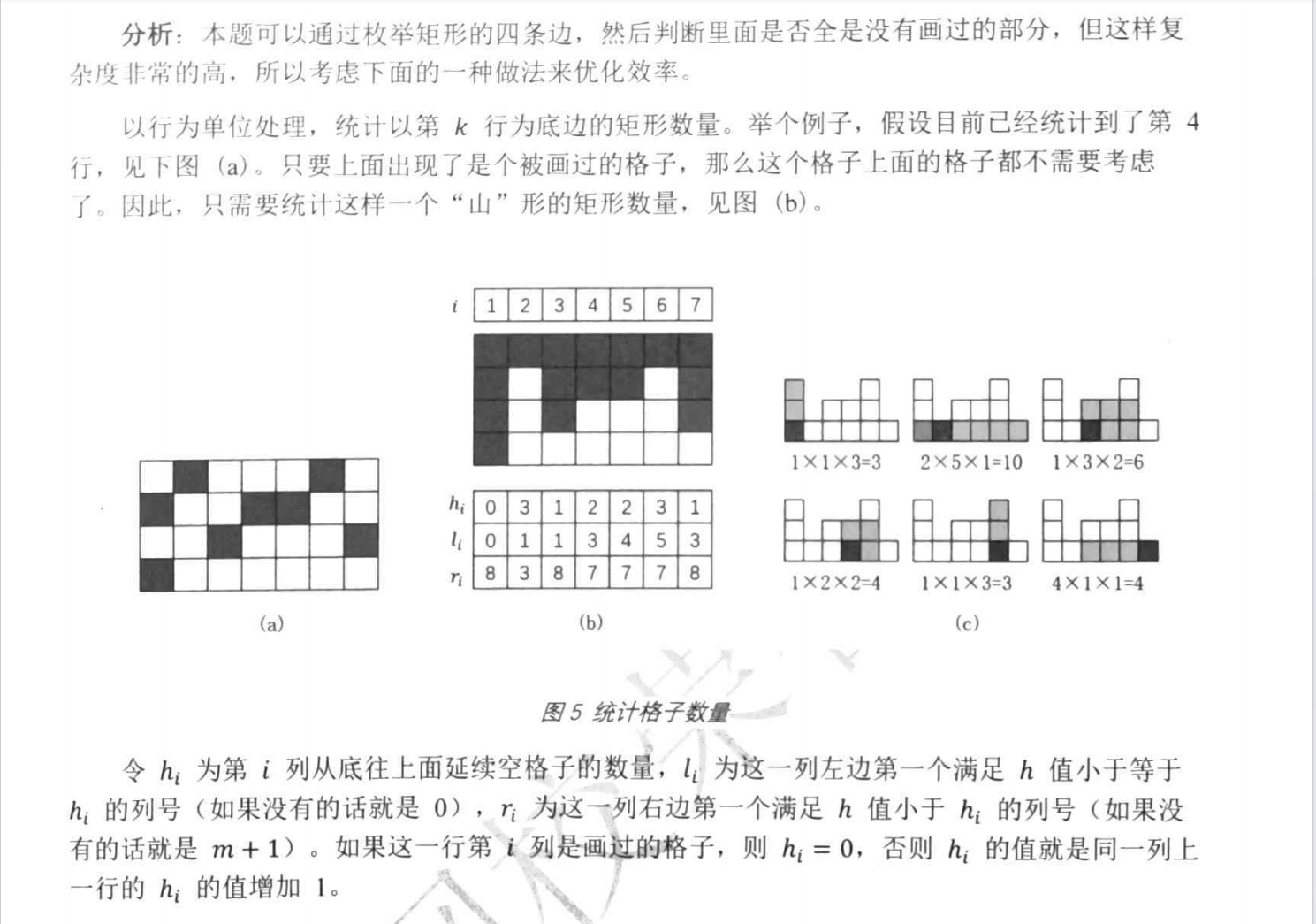
明白了这些后,再看《深进》就懂啦~

1 | #include <bits/stdc++.h> |
本题是P4147的升级版,请先掌握该题;题目问有多少种剪矩形的办法。
根据悬线法可知,一个最大矩形可以由中线切开,组成的可能性 = 左半部分的可能性 * 右半部分的可能性
本题实际上就是求每个悬线向左和向右的最大扩展距离罢了~

但是要注意不重不漏哟,如下图所示:
A向右扩展时可以和P4147一样正常找最大
B向左扩展时遇到高度小于等于时就终止,因为A向右扩展时已经找过最大值了

明白了这些后,再看《深进》就懂啦~

