考点
题解
见思路
思路
线性动态规划
设dp[i]的含义为:
以a[i]为结尾的连续序列里,连续序列和的极大值
显然能得到状态转移方程: \[
dp\left[ i \right] =\max \left( dp\left[ i-1 \right] +a\left[ i \right]
,a\left[ i \right] \right) ,2\leqslant i\leqslant n
\] 直接编程即可:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 50;
int n, ans, a[maxn], dp[maxn];
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
ans = dp[1] = a[1];
for (int i = 2; i <= n; ++i) {
dp[i] = max(dp[i - 1] + a[i], a[i]);
ans = max(ans, dp[i]);
}
cout << ans;
return 0;
}
|
分治
考虑最大子段和出现的位置:
- 只出现在左半部分,不包含中线;
- 只出现在右半部分,不包含中线;
- 包含中线。
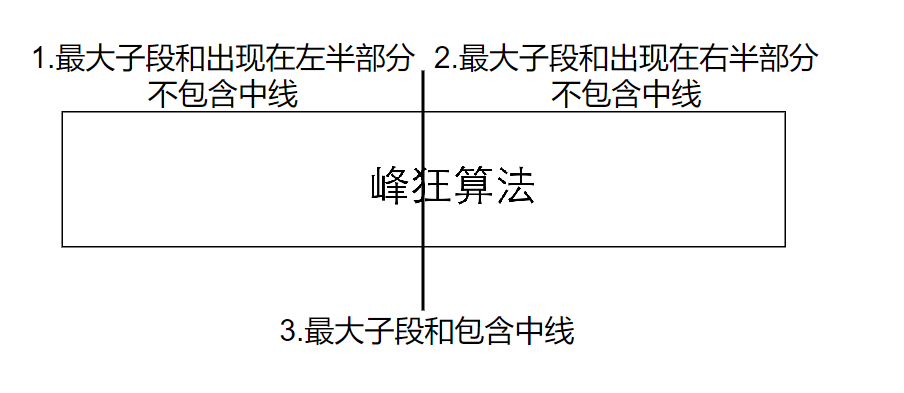
前两种可能分治处理即可,重点是第三种可能。
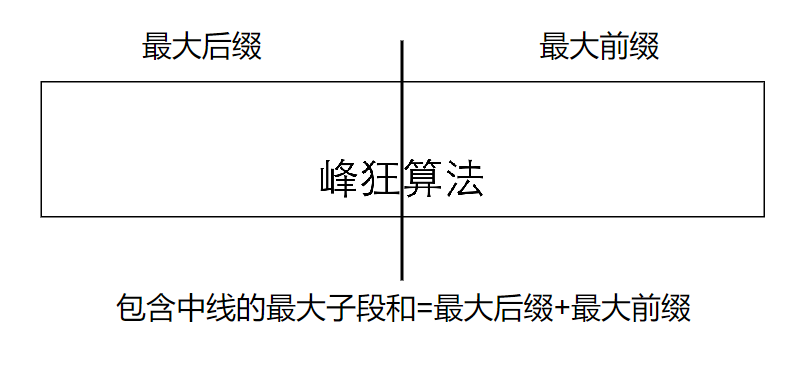
由于一定要经过中线,可以从中线开始向两边走;
分别取左半部分的最大后缀和右半部分的最大前缀后相加即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 50, mi = 0xc0c0c0c0;
int n, ans = mi, a[maxn];
void f(int l, int r) {
if (l == r) {
ans = max(ans, a[l]);
return;
}
int mid = r + ((l - r) >> 1);
int lsm = 0, rsm = 0, lmx = mi, rmx = mi;
for (int i = mid; i >= l; --i) lsm += a[i], lmx = max(lmx, lsm);
for (int i = mid + 1; i <= r; ++i) rsm += a[i], rmx = max(rmx, rsm);
ans = max(ans, lmx + rmx);
f(l, mid), f(mid + 1, r);
}
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
f(1, n);
cout << ans;
return 0;
}
|

