P2789 直线交点数

发表于 分类于 阅读次数： Waline： 本文字数： 390 阅读时长 ≈ 1 分钟

考点

  • 排列组合

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
using namespace std;
const int LEN = 1e3 + 50;
bool vis[LEN];
int n, ans, arr[LEN];

void dfs(int pre, int idx, int sum) {
  if (idx > n || sum > n) return;
  if (sum == n) {
    int cnt = arr[0], tot = 0;
    for (int i = 1; i < idx; ++i) tot += arr[i] * cnt, cnt += arr[i];
    if (!vis[tot]) ++ans;
    vis[tot] = 1;
    return;
  }
  for (int i = pre; i <= n; ++i) {
    arr[idx] = i;
    dfs(i, idx + 1, sum + i);
  }
}

int main() {
  cin >> n;
  dfs(1, 0, 0);
  cout << ans;
  return 0;
}

思路

无三线共点的含义是，当前直线要么与其他直线相交产生新的交点，要么与其他直线平行

根据这一特性，考虑采用分组的方式将情况分类

假设(x)代表该组内有x条直线平行，不在一个组内的直线相交

比如(2)、(3)代表第1个组内有2条直线平行，第2个组内有3条直线平行

第1个组与第2个组相交，得到2 * 3 = 6个交点

接下来以样例n == 4举例，有{0、3、4、5、6}共5种交点数

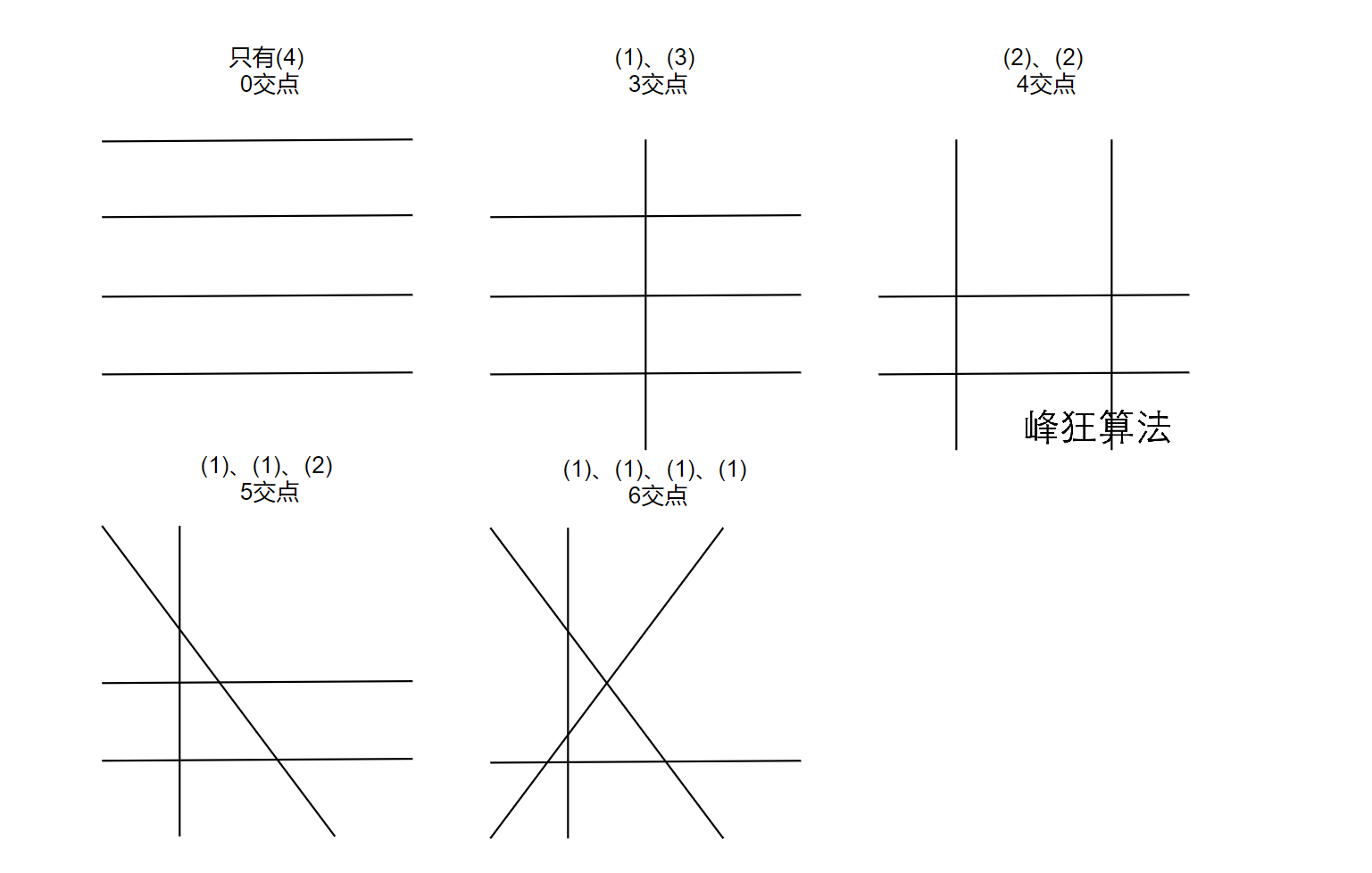
通过观察可以发现，实际上就是对整数n进行拆分，对每一种可行的拆分方案执行如下操作：

假设有拆分方案arr={1,1,2}，实际上就是(1)、(1)、(2)

令初始时cnt = 1 = arr[0]，记录需要被交的直线个数；tot记录交点数

从arr[1]开始，此时arr[1] * cnt = 1 * 1 = 1，tot += 1，cnt += arr[1]

代表(1)已与(1)相交

走到arr[2]，此时arr[2] * cnt = 2 * 2 = 4，tot += 4

代表(2)已与(1)、(1)相交