P2822. 组合数问题

发表于 2023-12-07 更新于 2023-12-12 分类于洛谷阅读次数： Waline：本文字数： 496 阅读时长 ≈ 2 分钟

考点

排列组合

题解

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int LEN = 2e3 + 50;
ll k, C[LEN][LEN], s[LEN][LEN];

ll f(int x, int y) { return x < 0 || y < 0 ? 0 : s[x][y]; }

void init() {
  // 杨辉三角求组合数C_{i}^{j}
  memset(C, -1, sizeof(C));
  for (int i = 0; i <= 2000; ++i) {
    C[i][0] = C[i][i] = 1;
    for (int j = 1; j < i; ++j) {
      C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % k;
    }
  }
  // 二维前缀和
  for (int i = 0; i <= 2000; ++i) {
    for (int j = 0; j <= 2000; ++j) {
      s[i][j] =
          f(i - 1, j) + f(i, j - 1) - f(i - 1, j - 1) + (C[i][j] == 0 ? 1 : 0);
    }
  }
}

int main() {
  int t, n, m;
  cin >> t >> k;
  init();
  while (t--) {
    cin >> n >> m;
    cout << s[n][m] << endl;
  }
  return 0;
}

思路

求解组合数的模板题，先根据《深基》的几张图来回顾一下杨辉三角吧

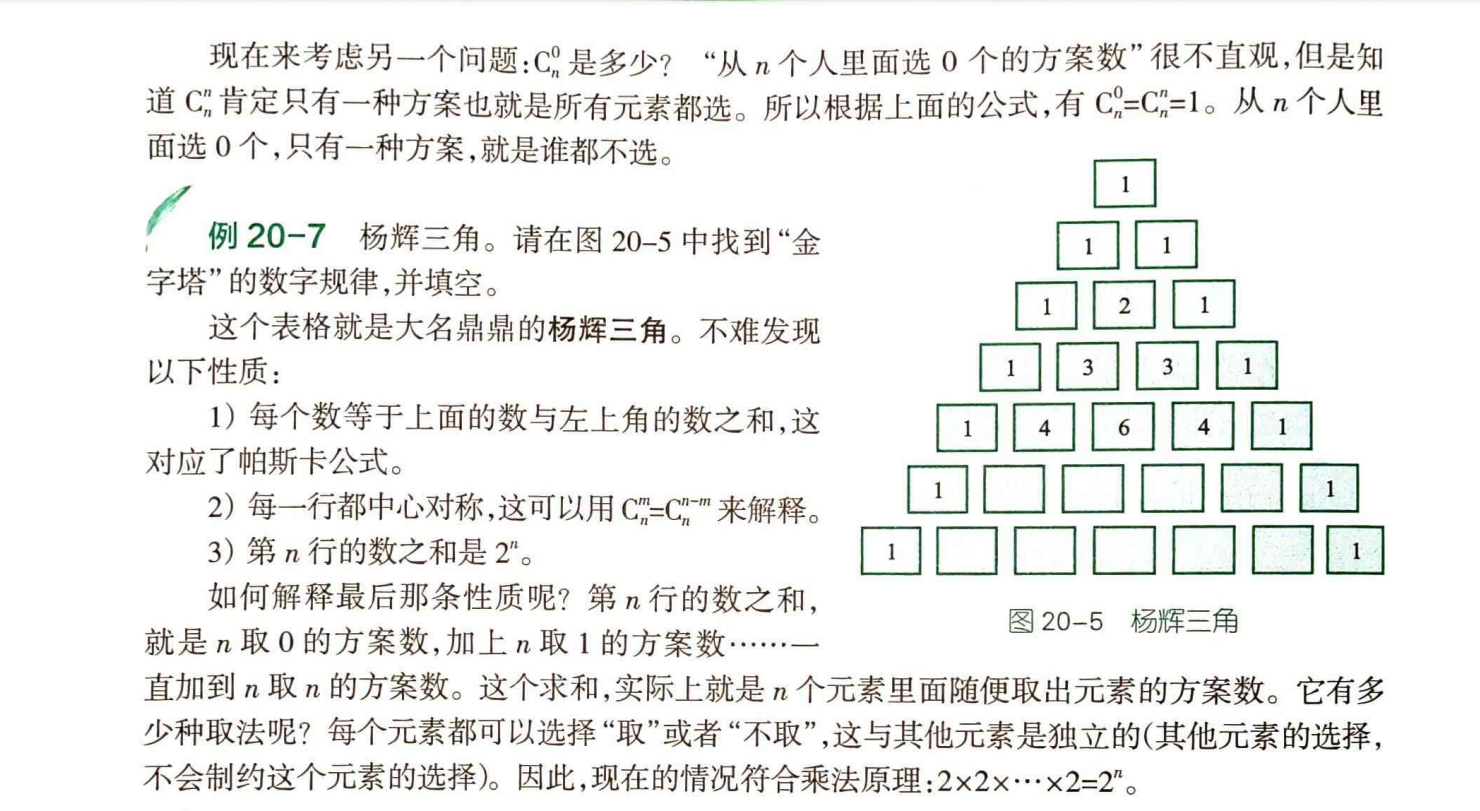
先将2000以内的组合数打表求出

那样数字会过于庞大，好在题意是求能否整除k；所以每次只保存模k的值即可（模运算不影响加法乘法）

当然，组合数数组需要初始化为-1而不是常规的0，否则不能确定到底是模k后得到的0还是初始就是0

从杨辉三角的视角看，题目每次询问的是二维数组某一区间内，模k后为0的组合数个数

所以用二维前缀和再次打表！

比如n = 3, m = 3, k = 2的话，求\(\left\{ C_{0}^{0},C_{1}^{0},C_{1}^{1},C_{2}^{0},C_{2}^{1},C_{2}^{2},C_{3}^{0},C_{3}^{1},C_{3}^{2},C_{3}^{3} \right\}\)中模k后等于0的个数

用帕斯卡公式求出的组合数数组