考点
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <bits/stdc++.h>
using namespace std;
const int LEN = 10e5 + 50;
int n, fa[LEN], dis[LEN], sz[LEN];
int find(int x) {
if (fa[x] == x) return x;
int anc = fa[x];
fa[x] = find(fa[x]);
dis[x] += dis[anc];
return fa[x];
}
void join(int x, int y) {
int a = find(x), b = find(y);
fa[a] = b;
dis[a] = sz[b];
sz[b] += sz[a];
}
int main() {
char ch;
int x, y;
cin >> n;
for (int i = 1; i <= n; ++i) fa[i] = i, sz[i] = 1;
for (int i = 1; i <= n; ++i) {
cin >> ch >> x >> y;
if (ch == 'M') {
join(x, y);
} else if (ch == 'C') {
if (find(x) != find(y))
cout << "-1" << endl;
else
cout << abs(dis[x] - dis[y]) - 1 << endl;
}
}
return 0;
}
|
思路
题目要求两结点中间有多少个结点,令dis[x]为x走到祖宗结点的所需步数
这样一来,abs(dis[x] - dis[y])就能得到x走到y的所需步数,再减去到达y的那一步
最终要求的就是abs(dis[x] - dis[y]) - 1
题目要求结点之间的个数,不含两结点本身
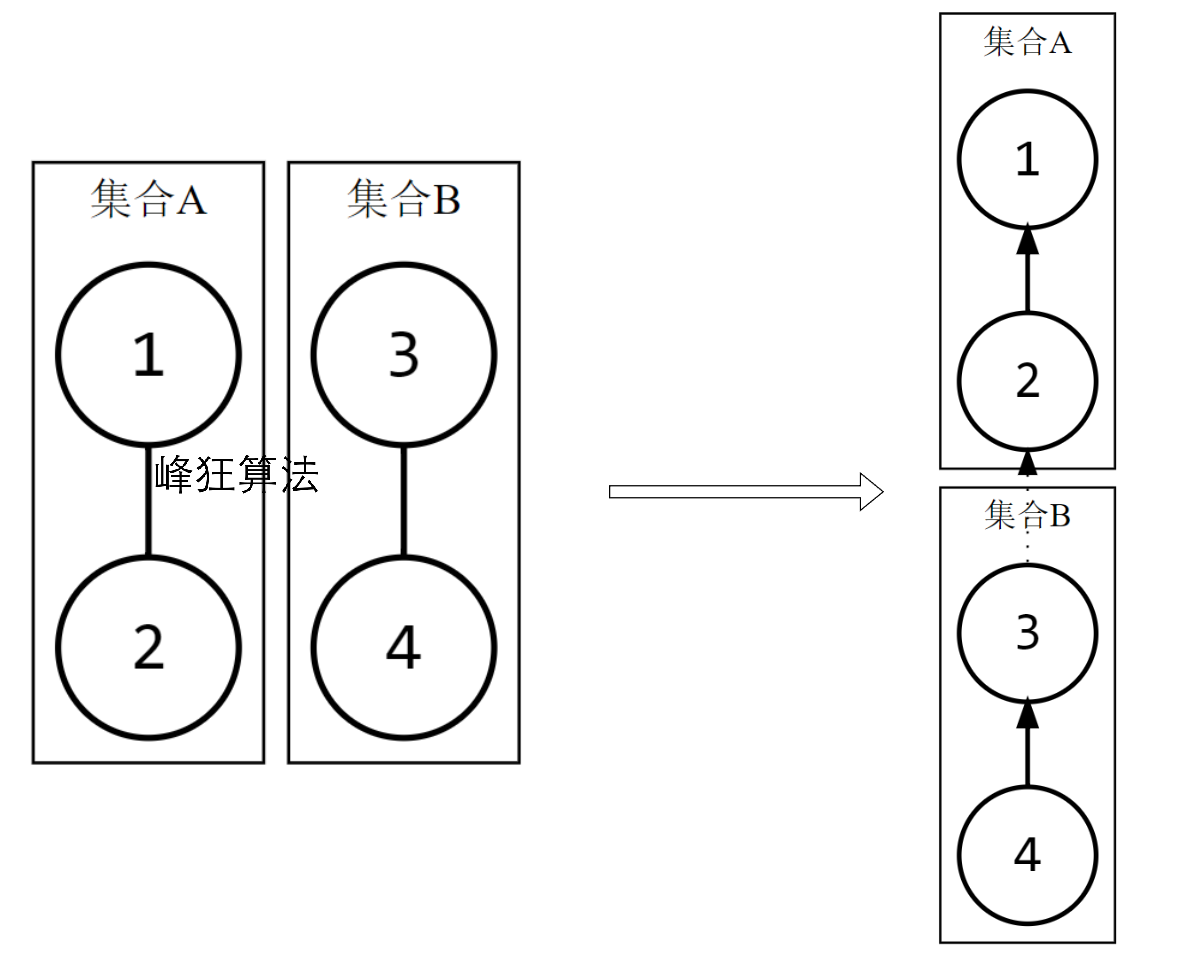
先考虑路径压缩部分。由于并查集合并时只会修改祖宗结点
那么结点3的步数可以直接从0修改到集合A的大小,令sz[x]为x为祖先时,其内部的集合大小
即dis[3] = sz[1] = 2
但是dis[4]仍等于1,还是处在以3为祖先情况下尚未更新
所以应该有新dis[4] = 原dis[4] + 更新后的dis[3]
再考虑合并部分。
方才提到,可以直接令结点3的步数赋值为集合A的大小,结合路径压缩就可以更新集合B的所有子结点
修改完结点3后,再更新集合A的大小sz[1] = sz[1] + sz[3]