P3916 图的遍历

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 467 阅读时长 ≈ 2 分钟

考点

  • 强连通分量

题解

见思路

思路

DFS

如果直接对每个点都做一次DFS，肯定超时

考虑在DFS的过程中做优化。设DFS函数f(x)为x能到达的编号最大的点

显然有f(1) = max(1, f(2))，f(2) = max(2, f(4))，f(4) = max(4, f(3))，f(3) = 3

这样一来，在回溯的过程中就能一并处理同一路径的其他结点，避免重复计算

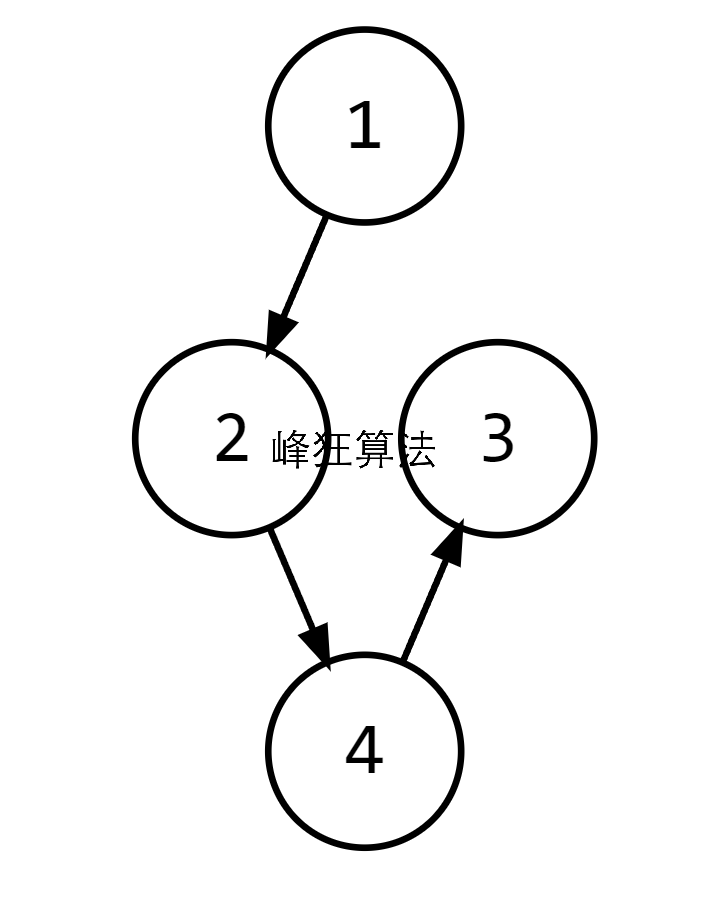
但是，图论的题目得当心是否存在环；本题并没有说排除环这一情况，如下图的一个环

f(1) = max(1, f(2))，f(2) = max(2, f(4))，f(4) = max(4, f(3))，f(3) = max(3, f(1))

如果按照上述思路，f(3)最终会拿自己和未更新的f(1)进行相比，得到错误的f(3) = 3，但实际上f(3) = 4

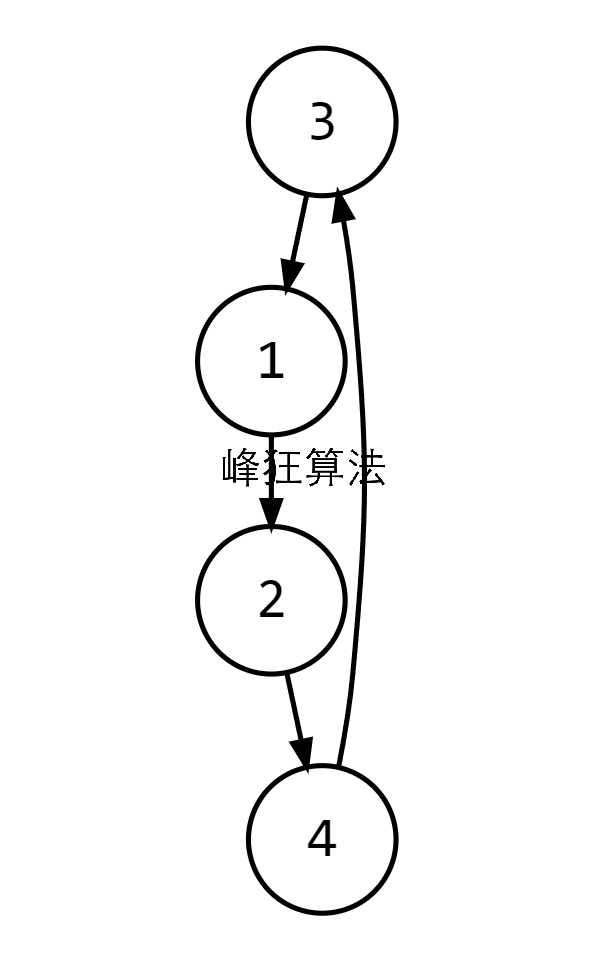
所以转变一下思路，之前是让点自己去找它能到达的最大的点，现在让最大的点去告诉哪些点能到达它

用反向边建图，若原图中有一条边是u -> v，我们就建反向的边v -> u

从编号大的结点v开始DFS，更新所经路径上没有被更新过的结点为v即可

因为从n枚举到1时，被更新过的点一定是用比当前数字大的点更新的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>
using namespace std;
const int LEN = 2e5 + 50;
int n, m, val[LEN];
//标志数组，走过的结点不再走
bool vis[LEN];
vector<int> e[LEN];

void dfs(int x, int mx) {
  if (vis[x]) return;
  val[x] = mx, vis[x] = true;
  for (int i = 0, sz = e[x].size(); i < sz; ++i) dfs(e[x][i], mx);
}

int main() {
  int x, y;
  cin >> n >> m;
  for (int i = 1; i <= m; ++i) {
    cin >> x >> y;
    e[y].emplace_back(x);
  }
  for (int i = n; i >= 1; --i) dfs(i, i);
  for (int i = 1; i <= n; ++i) cout << val[i] << " ";
  return 0;
}