P1185. 绘制二叉树

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 1.3k 阅读时长 ≈ 4 分钟

考点

  • 二叉树
  • 模拟

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
using namespace std;
const int LEN = 10240;
char ans[LEN][LEN]; //记录答案
bool del[LEN][LEN]; //一维记录被删结点的层次，二维记录被删结点的名次
int width, height, m, n;

struct Node
{
    //横纵坐标，层次，在树中的下标
    //左孩子的下标等于 父结点 * 2
    //右孩子的下标等于 父结点 * 2 + 1
    int x_, y_, lv_, id_;
    Node(int x, int y, int lv, int id) : x_(x), y_(y), lv_(lv), id_(id) {}
};

queue<Node> q;

//孩子结点往父亲结点方向，填充斜杠
void filling(int x, int y, bool lft, int cnt)
{
    if (lft)
    {
        for (int i = 1; i <= cnt; ++i)
            ans[x + i][y + i] = '/';
    }
    else
    {
        for (int i = 1; i <= cnt; ++i)
            ans[x + i][y - i] = '\\';
    }
}

void bfs()
{
    while (!q.empty())
    {
        Node u = q.front();
        q.pop();
        //即将填充的斜杠个数
        int cnt = u.lv_ == m - 1 ? 1 : 3 * pow(2, m + 1 - u.lv_ - 3) - 1;
        //左孩子的信息
        int lx = u.x_ - (cnt + 1), ly = u.y_ - (cnt + 1), llv = u.lv_ + 1, lid = u.id_ * 2;
        //右孩子的信息
        int rx = u.x_ - (cnt + 1), ry = u.y_ + (cnt + 1), rlv = u.lv_ + 1, rid = u.id_ * 2 + 1;
        //如果左孩子不被删除
        if (!del[llv][lid - (1 << u.lv_) + 1])
        {
            ans[lx][ly] = 'o';
            //填充斜杠
            filling(lx, ly, true, cnt);
            //如果左孩子是最后一层，说明它是叶子结点没有孩子，就没必要塞入队列
            if (llv != m)
                q.emplace(lx, ly, llv, lid);
        }
        if (!del[rlv][rid - (1 << u.lv_) + 1])
        {
            ans[rx][ry] = 'o';
            filling(rx, ry, false, cnt);
            if (rlv != m)
                q.emplace(rx, ry, rlv, rid);
        }
    }
}

int main()
{
    int level, idx;
    cin >> m >> n;
    //如果只有一层，即根结点，直接输出即可
    //因为不可能删除根结点
    if (m == 1)
    {
        cout << 'o';
        return 0;
    }
    memset(ans, ' ', sizeof(ans));
    while (n--)
    {
        cin >> level >> idx;
        del[level][idx] = true;
    }
    //计算整棵树的宽度与高度
    width = 6 * pow(2, m - 2) - 1, height = 3 * pow(2, m - 2);
    //加入根结点
    q.emplace(height - 1, (width - 1) / 2, 1, 1);
    ans[height - 1][(width - 1) / 2] = 'o';
    bfs();
    for (int x = height - 1; x >= 0; --x, cout << endl)
        for (int y = 0; y < width; ++y)
            cout << ans[x][y];
    return 0;
}

思路

具体实现细节见代码，主要阐述一下编程思维

很容易想到实现流程：

  • 最终要输出结果，所以需要二维数组ans来保存

    还要一个标志数组del记录第几层的第几个结点需要被删除

  • 从根结点开始，递归地处理左子树与右子树

    左右子树的处理次序与答案不相关，DFS或BFS的实现也与答案不相关；因为本身其实是一颗满二叉树

    但这种按层次处理的二叉树问题，显然用BFS能极大降低思维难度

  • 若用BFS实现

    每次当前的父结点判断左右孩子是否需要被删除：

    • 需要被删除的就不填充斜杠与孩子结点

    • 保留的孩子则填充与父结点之间的斜杠；若孩子所处不在最后一层，就将其添加进队列进行下一轮扩展

      （最后一层是叶子结点，没有孩子，扩展啥）

答案的存储样式如下：

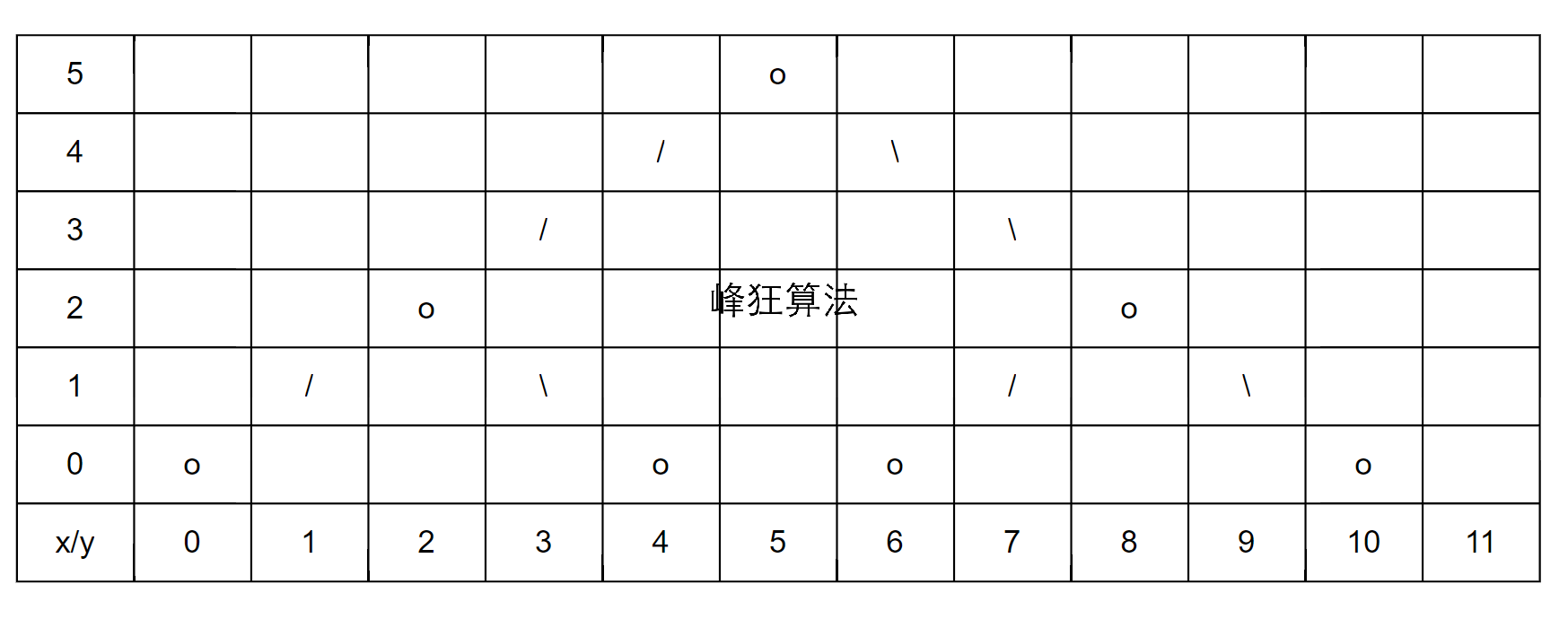
先找找x轴，即二叉树的高度height的规律

m height
1 1
2 3
3 6
4 12

得到\(height=3\times 2^{m-2}\)这一规律，其中m = 1只有根结点的时候特判即可

接下来找y轴，二叉树的宽度width的规律

m width
1 1
2 5
3 11
4 23

得到\(width=6\times 2^{m-2}-1\)这一规律，同样m = 1时特判

根结点的位置规律：\(\text{横坐标}x=height-1\)，\(\text{纵坐标}y=\frac{width-1}{2}\)

由于满二叉树的对称性，尽管题目没有给出其他层数的数据，但知道根结点就能在草稿纸上推斜杠的规律

正常情况下根结点所在层次定义为第一层，但是斜杠的规律就不好找；所以定义叶子结点为固定的第一层

设当前层次为lv，斜杠数定义为当前层次的父结点与其左或右孩子中间的斜杠数

比如lv = 3，此时斜杠数等于第3层的父结点与第2层的左或右孩子中间的斜杠数

lv 斜杠数
1 0
2 1
3 2
4 5
5 11
6 23

得到\(\text{斜杠数}=3\times 2^{lv-3}-1\)，lv等于2时特判

这是叶子结点为第一层时的定义，需要将其转换为根结点为第一层的定义：\(\text{斜杠数}=3\times 2^{m+1-lv-3}-1\)

你可以自己发现一下规律，有数组{1, 2, 3, 4}

要变成{4, 3, 2, 1}要如何做呢？

每个元素被5减不就好了嘛~

如何断定当前结点是该层的第几个呢？

假设根结点的下标为1，以顺序存储的办法

那么左孩子的下标为父结点下标 * 2，右孩子的下标为父结点下标 * 2 + 1

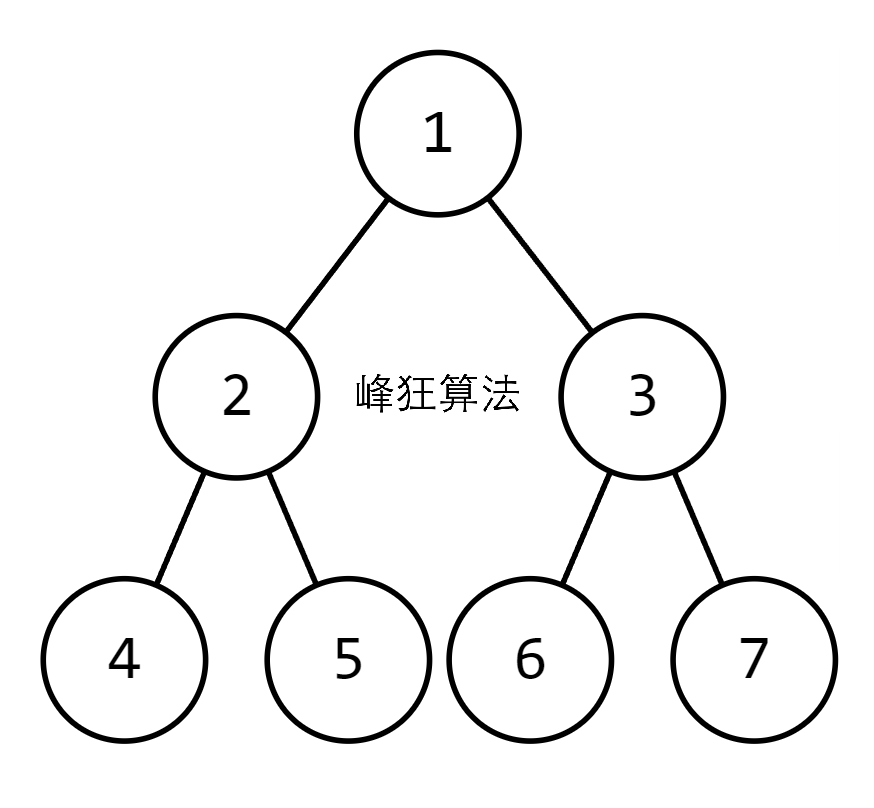
假设当前为k + 1层，下标为id；根据满二叉树的性质，本层之前共有\(2^k-1\)个结点

那么该节点在本层的次序，不就等于\(id-\left( 2^k-1 \right)\)嘛