P4913. 二叉树深度

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 308 阅读时长 ≈ 1 分钟

考点

  • 二叉树

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
using namespace std;
const int LEN = 1e6 + 50;
int N;

struct Node
{
    int lc_, rc_;
} arr[LEN];

#define rt arr[root]

int dfs(int root)
{
    if (!root)
        return 0;
    return max(dfs(rt.lc_), dfs(rt.rc_)) + 1;//根结点的深度 = 左右子树的最大深度 + 根结点本身
}

int main()
{
    cin >> N;
    for (int i = 1; i <= N; ++i)
        cin >> arr[i].lc_ >> arr[i].rc_;
    cout << dfs(1);
    return 0;
}

思路

题目每次是按照结点编号增加子结点的，如果按照顺序存储，估算一下数组大小：

  • 1结点的子结点若是2，那么2的下标是1结点的下标 * 2 = 2
  • 2结点的子结点若是3，那么3的下标是2结点的下标 * 2 = 4
  • 3结点的子结点若是4，那么4的下标是3结点的下标 * 2 = 8
  • 如此类推，1e6节点的下标是21e6，任何类型的数组都存不下

上述是二叉树的一种极端情况，退化成了一条链

此时树的深度等于结点个数n，若采用顺序存储需要建立一个大小为2n的数组

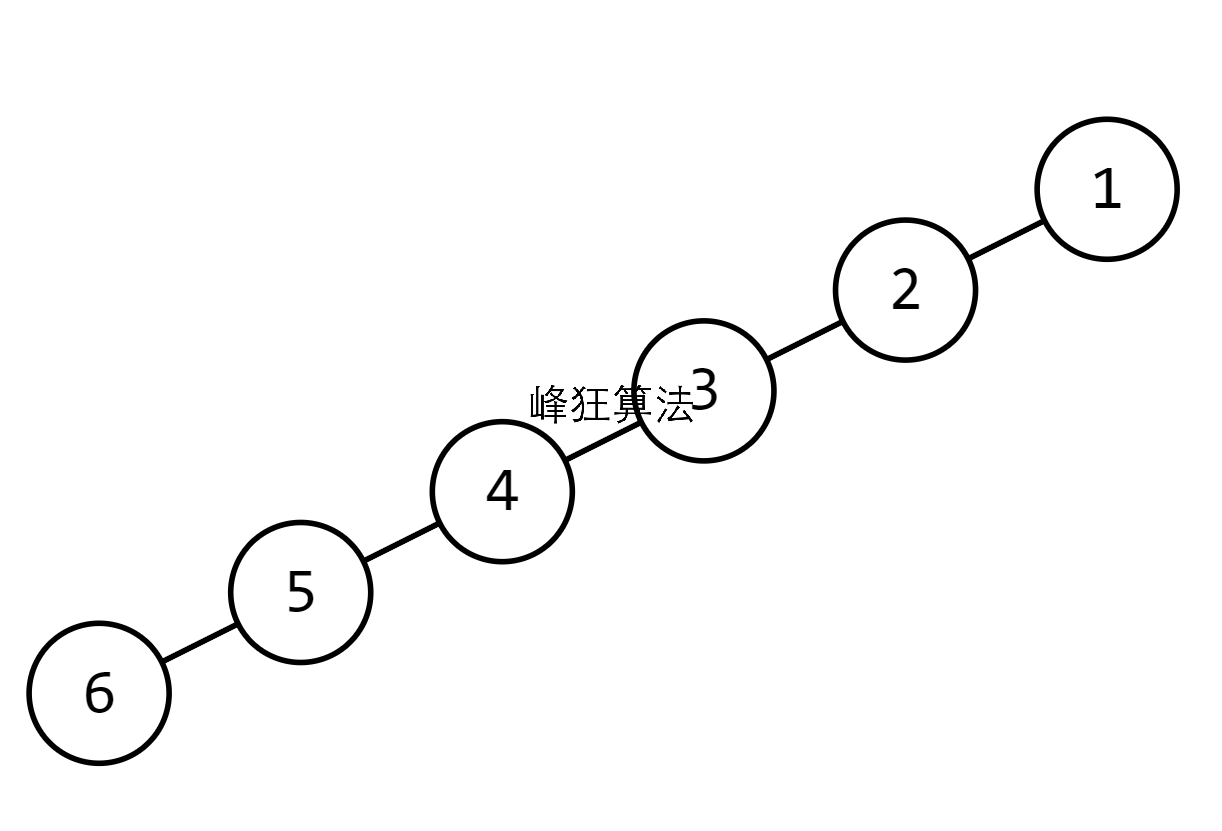
所以需要用链式存储，用结构体记录左右孩子的位置