P5019. 铺设道路

发表于 2023-10-13 更新于 2023-10-25 分类于洛谷阅读次数： Waline：本文字数： 910 阅读时长 ≈ 3 分钟

考点

贪心

题解

#include <bits/stdc++.h>

using namespace std;

const int LEN = 1e5 + 10;

int arr[LEN];

int main()
{
    int n, ans = 0;
    cin >> n;
    for (int i = 0; i < n; ++i)
        cin >> arr[i];
    ans = arr[0];
    for (int i = 1; i < n; ++i)
    {
        if (arr[i] > arr[i - 1])
            ans += arr[i] - arr[i - 1];
    }
    cout << ans;
    return 0;
}

思路

绝对经典的超级贪心好题！

考虑以下情况

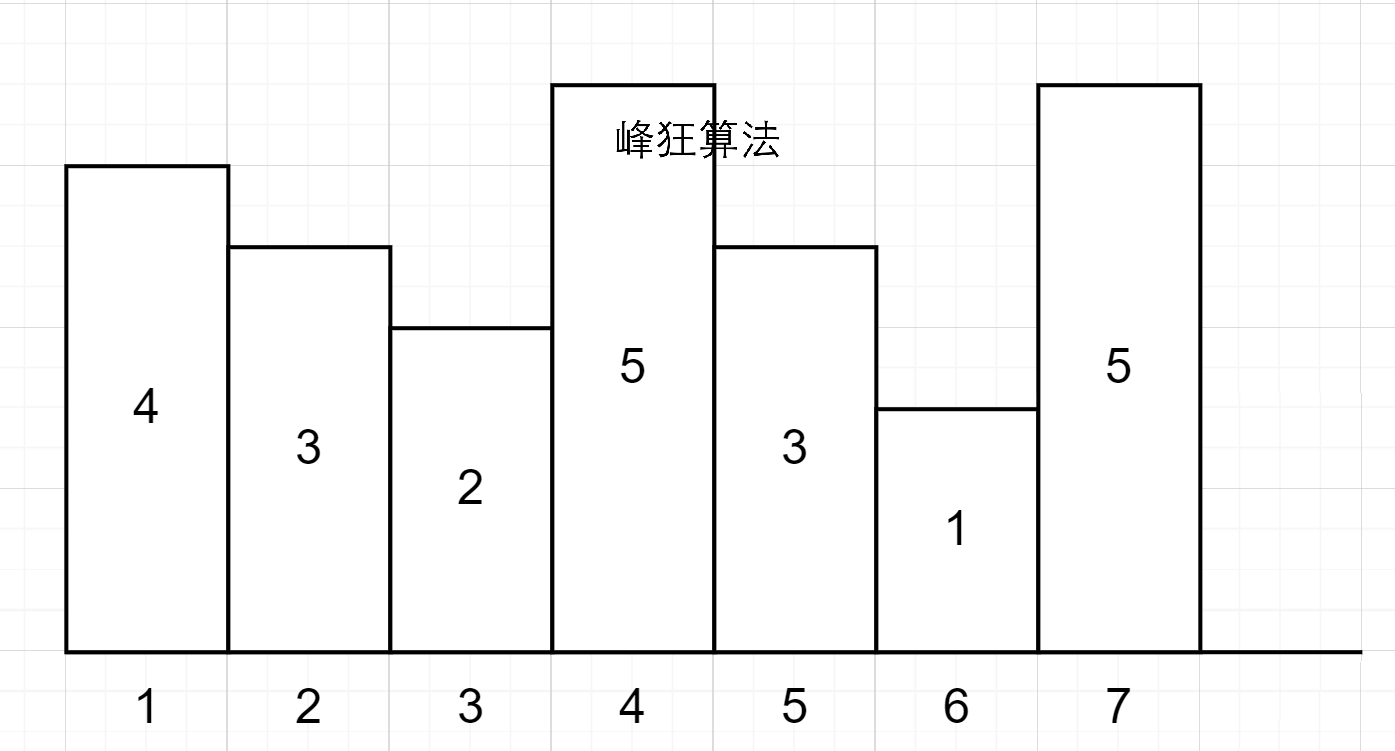
正常思路，每次找到最小的深度，并将其所在的连续区间一起填平....线段树都搞不定的啊，绝对超时

先按照题意模拟一遍：

6号位填平，1-7号位一起减1，天数加1

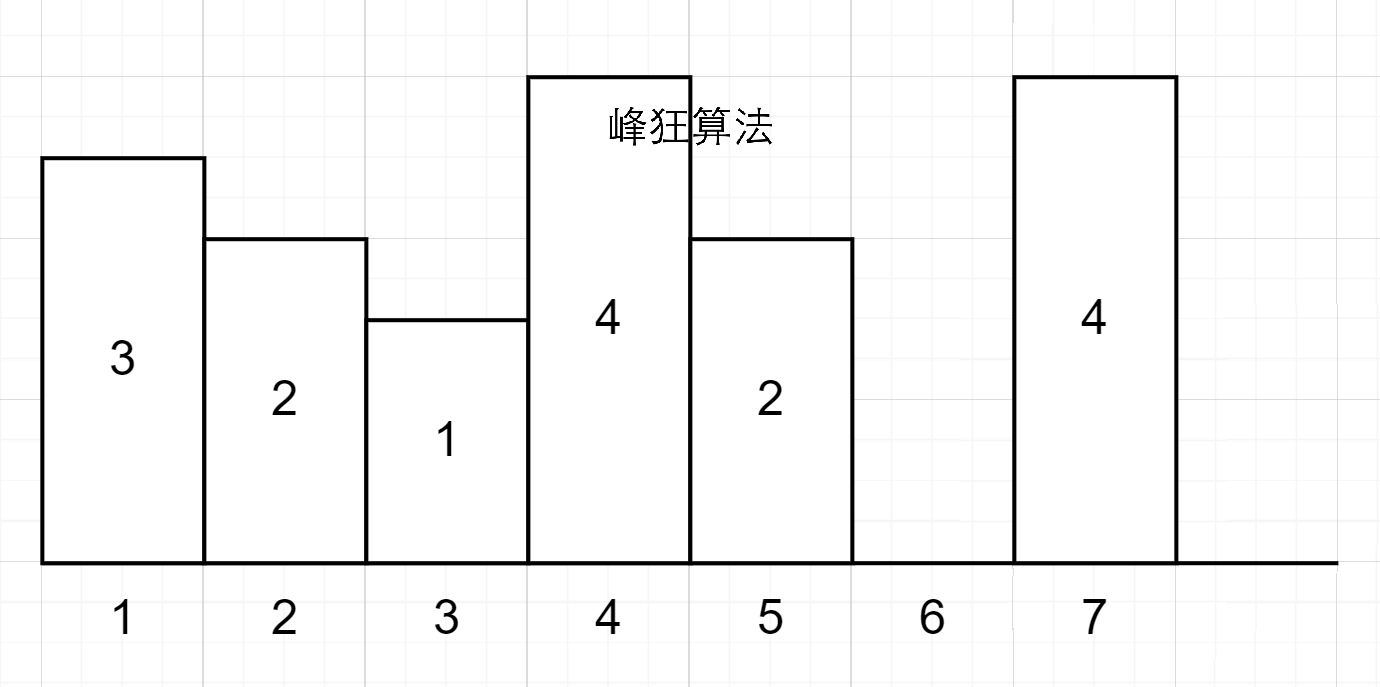
3号位填平，1-5号位一起减1，天数加1

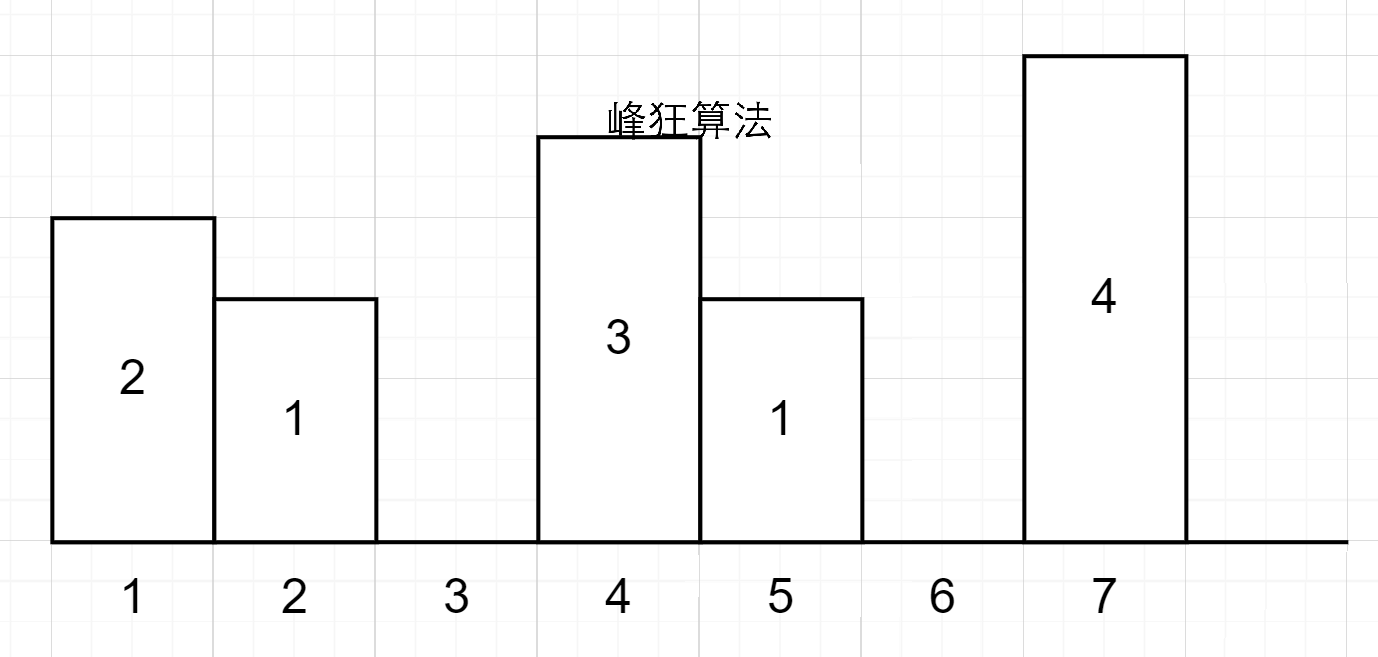
然后1-2号位需要2天，4-5号位需要2天，7号位需要4天；一共的开销如下： \[ \underset{\text{填平}6\text{号}}{1}+\underset{\text{填平}3\text{号}}{1}+\underset{\text{填平}1-2\text{号}}{2}+\underset{\text{填平}4-5\text{号}}{3}+\underset{\text{填平}7\text{号}}{4} \] 显然可以发现，降序的连续序列的天数开销，取决于最大的那一位；所以作图如下：

1-3号位组成的降序序列A，天数取决于1号位
4-6号位组成的降序序列B，天数取决于4号位
7号位组成的降序序列C，天数取决于7号位

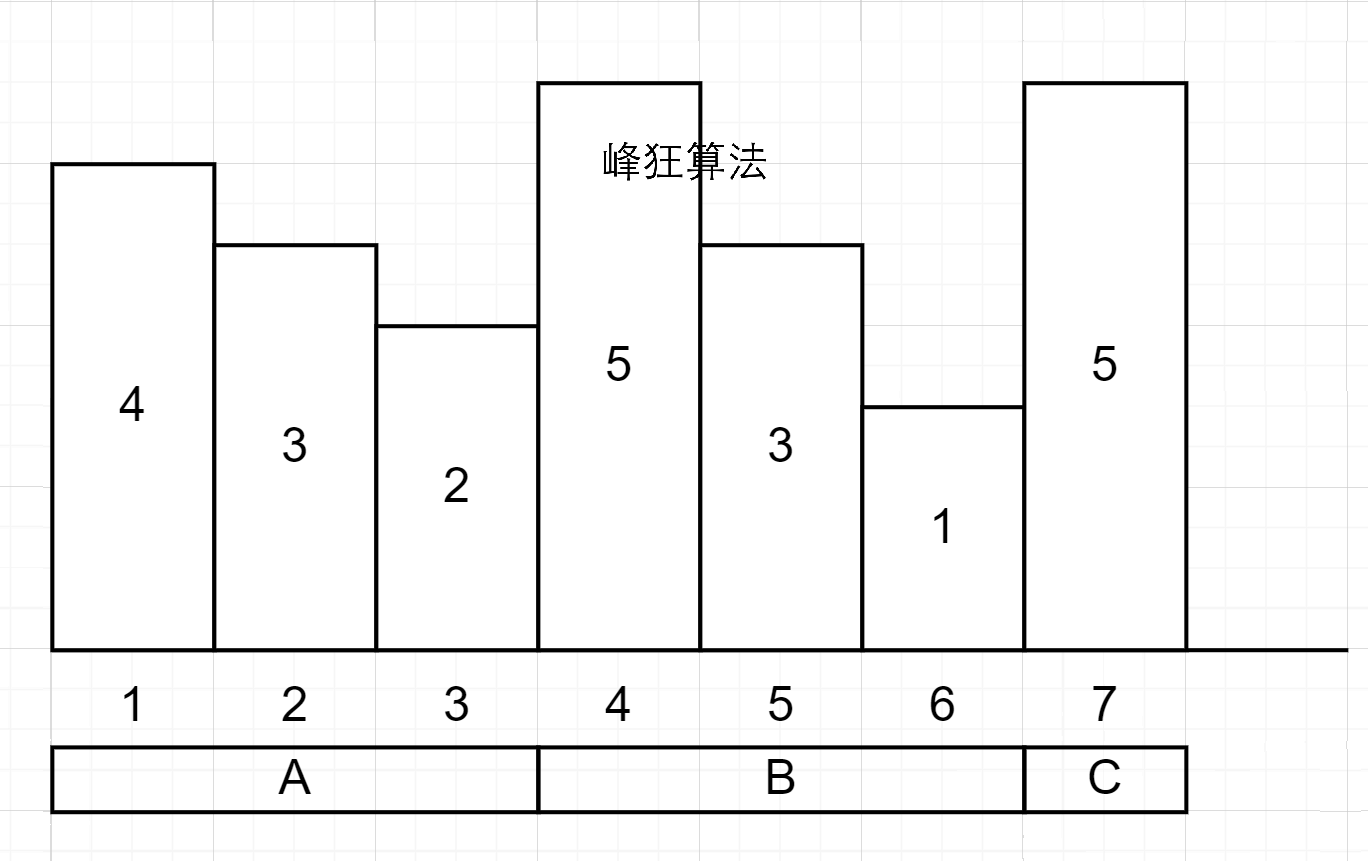
得知A、B、C内部的天数开销还不算完，A过渡到B序列中间那部分的升序序列开销还需要计算，即3号位到4号位

3号位填平了2个单位，作为与3号位连续的4号位，也会被填平2个单位，还有5 - 2 = 3个单位需要被填平，即3天

又由于4号位代表的就是整个B序列的天数开销，所以B序列的开销就是3天；同理6-7号位的升序序列，开销为5 - 1 = 4天

整体的开销如下： \[ \underset{A\text{序列的开销}}{4}+\underset{B\text{序列的开销}}{3}+\underset{C\text{序列的开销}}{4} \] 接下来难度升级一下，如果输入是{4, 3, 2, 5, 6, 1, 5}呢？答案是多少天？

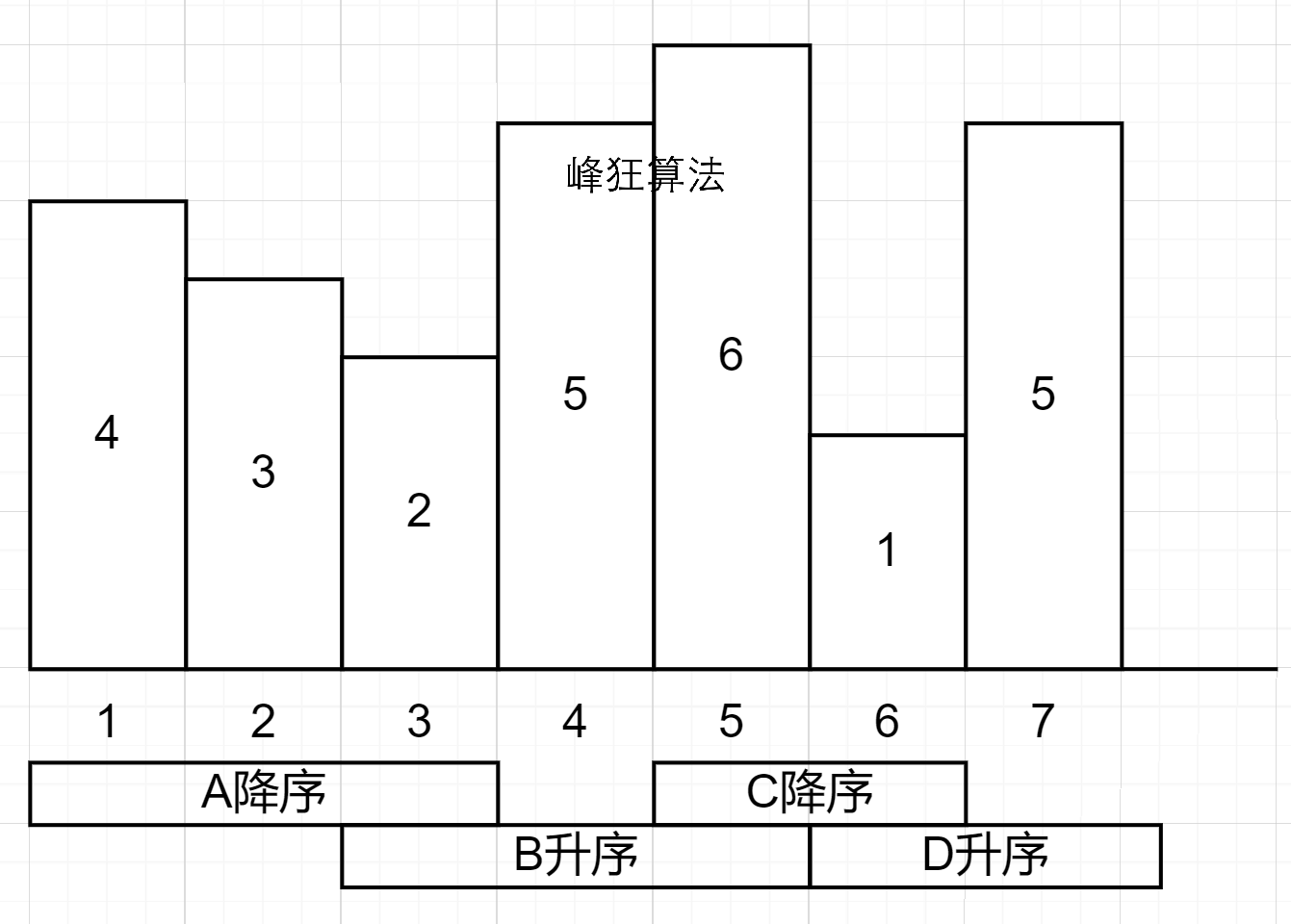
A降序部分取决于1号位

而1号位之前没有东西，那么A降序开销即为4天
B升序这部分，3号位给4号位填平了2个单位，那么4号位还剩5 - 2 = 3天

3、4号位一共给5号位填平了5个单位，那么5号位还剩6 - 5 = 1天

所以B升序开销为3 + 1 = 4天
C降序这部分取决于5号位，而刚才B升序已经计算了5号位的开销，所以C降序不作计算
D升序这部分，6号位给7号位填平了1个单位，7号位还剩5 - 1 = 4天

所以D升序开销为4天
共计4 + 4 + 4 = 12天