P4924. 魔法少女小Scarlet

发表于 分类于 阅读次数： Waline： 本文字数： 477 阅读时长 ≈ 2 分钟

考点

  • 模拟

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>

using namespace std;

const int LEN = 501;

int N, ans[LEN][LEN], tmp[LEN][LEN];

void init()
{
    int cnt = 1;
    for (int i = 1; i <= N; ++i)
    {
        for (int j = 1; j <= N; ++j)
        {
            ans[i][j] = cnt++;
        }
    }
}

void print()
{
    for (int i = 1; i <= N; ++i, cout << endl)
    {
        for (int j = 1; j <= N; ++j)
        {
            cout << ans[i][j] << " ";
        }
    }
}

void rotate(int c_x, int c_y, int r, int z)
{
    copy(&ans[0][0], &ans[0][0] + LEN * LEN, &tmp[0][0]);
    if (z == 0)
    {
        // 顺时针
        for (int i = -r; i <= r; ++i)
        {
            for (int j = -r; j <= r; ++j)
            {
                tmp[c_x + j][c_y - i] = ans[c_x + i][c_y + j];
            }
        }
    }
    else
    {
        // 逆时针
        for (int i = -r; i <= r; ++i)
        {
            for (int j = -r; j <= r; ++j)
            {
                tmp[c_x - j][c_y + i] = ans[c_x + i][c_y + j];
            }
        }
    }
    copy(&tmp[0][0], &tmp[0][0] + LEN * LEN, &ans[0][0]);
}

int main()
{
    int m, c_x, c_y, r, z;
    cin >> N >> m;
    init();
    while (m--)
    {
        cin >> c_x >> c_y >> r >> z;
        rotate(c_x, c_y, r, z);
    }
    print();
    return 0;
}

思路

假设当前待旋转的矩阵中心c_x = 3，c_y = 3，r = 2

由于是围绕该中心旋转，所以不妨将子矩阵放在以该中心为原点的y - x坐标系中分析

数组中的上下移动与平面直角坐标系中的上下移动概念是相反的

若有点坐标(x, y)，要求向左走1次，向上走2次

在平面直角坐标系中，移动后的坐标为(x - 1, y + 2)

而在数组中，移动后的坐标为(x - 2, y - 1)

所以为了方便理解，令新的坐标系横坐标为y，即列号；纵坐标为x，即行号

以该子矩阵的点(1, 2)为例，分析它的顺时针路径图：

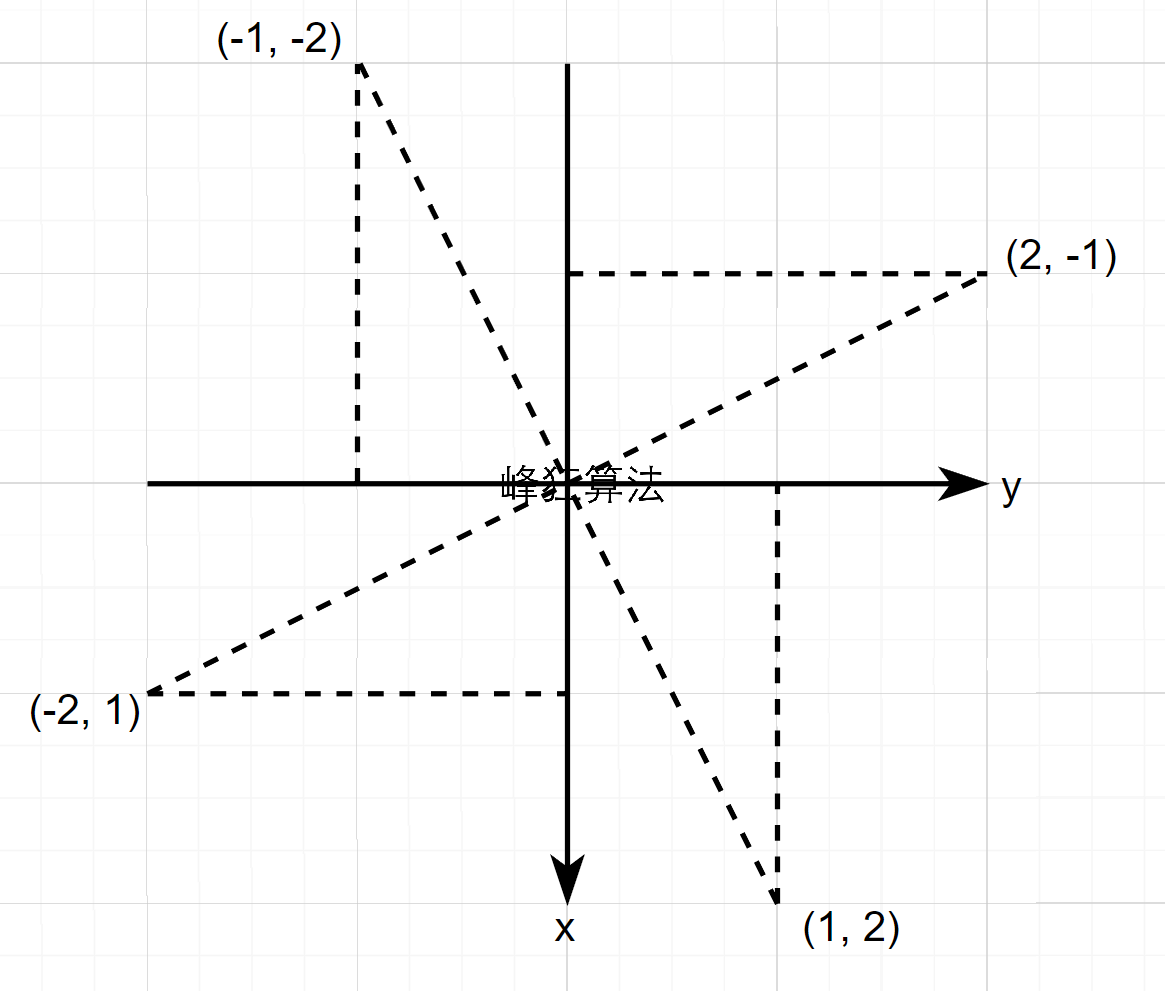
若令i，j分别为横纵坐标变化，可以发现顺时针变化的规律，即： \[ \left( y+i, x+j \right) \rightarrow \left( y-j, x+i \right) \\ \text{其中}i\in \left[ -r, r \right] , j\in \left[ -r, r \right] \] 同理逆时针规律也可以得到： \[ \left( y+i, x+j \right) \rightarrow \left( y+j, x-i \right) \\ \text{其中}i\in \left[ -r, r \right] , j\in \left[ -r, r \right] \]