P1480. A/B Problem

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 486 阅读时长 ≈ 2 分钟

考点

  • 高精度

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <bits/stdc++.h>

using namespace std;

const int LEN = 25000;

class BigInt
{
public:
    int len_;
    int arr_[LEN];
    int &operator[](int idx)
    {
        return arr_[idx];
    }
    BigInt(string s = "")
    {
        memset(arr_, 0, sizeof(arr_));
        len_ = s.length();
        for (int i = 1; i <= len_; ++i)
        {
            arr_[i] = s[len_ - i] - '0';
        }
    }
    void flatten(int len)
    {
        len_ = len;
        for (int i = 1; i <= len_; ++i)
        {
            if (arr_[i] < 0)
            {
                arr_[i + 1] -= 1;
                arr_[i] += 10;
            }
        }
        while (!arr_[len_])
            --len_;
    }
    void print()
    {
        for (int i = max(1, len_); i >= 1; --i)
        {
            cout << arr_[i];
        }
    }
};

//以lst_dg为最低有效位的a
bool greater_eq(BigInt a, int lst_dg, BigInt b)
{
    //a的位数比b的位数多
    if (a[lst_dg + b.len_] != 0)
        return true;
    for (int i = b.len_ - 1; i >= 0; --i)
    {
        if (a[lst_dg + i] > b[i + 1])
            return true;
        if (a[lst_dg + i] < b[i + 1])
            return false;
    }
    //a和b的值相等
    return true;
}

BigInt operator/(BigInt a, BigInt b)
{
    BigInt c;
    for (int lst_dg = a.len_ - b.len_ + 1; lst_dg >= 1; --lst_dg)
    {
        while (greater_eq(a, lst_dg, b))
        {
            for (int i = 0; i <= b.len_ - 1; ++i)
            {
                a[lst_dg + i] -= b[i + 1];
                if (a[lst_dg + i] < 0)
                {
                    a[lst_dg + i + 1] -= 1;
                    a[lst_dg + i] += 10;
                }
            }
            ++c[lst_dg];
        }
    }
    c.len_ = a.len_;
    while(c[c.len_] == 0)
        --c.len_;
    return c;
}

int main()
{
    string s1, s2;
    cin >> s1 >> s2;
    BigInt a(s1), b(s2);
    (a / b).print();
    return 0;
}

思路

与之前的高精度加减乘法由低位到高位的运算方向不同，高精度除法是从高位到低位运算

以175除以5为例子：

  • lst_dg初始位置为a.len_ - b.len_ + 1，确保以lst_dg为最低有效位的a长度等于b长度；随后从高位向低位遍历
  • 在lst_dg的遍历过程中，结合greater_eq函数判断当前以lst_dg为最低有效位的a是否大于除数b
  • 若大于，则执行高精减法，并更新商数组；循环这一操作，直到当前以lst_dg为最低有效位的a小于b

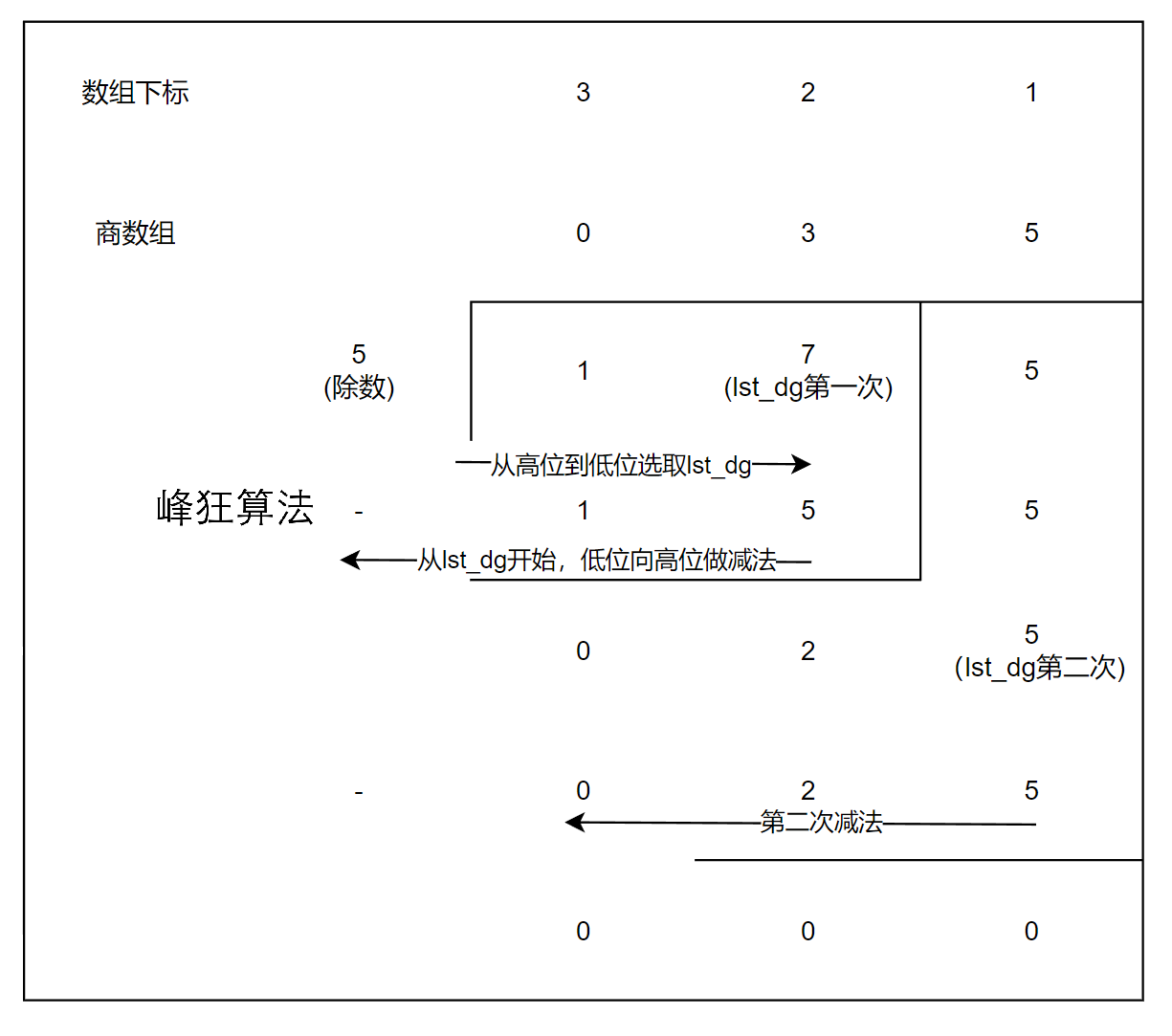
这里提一嘴高精度除低精度，非常简单：

1
2
3
4
5
6
7
8
9
10
11
12
BigInt operator/(BigInt a, int b)
{
    BigInt c;
    long long r = 0;
    for (int i = a.len_; i >= 1; --i)
    {
        c[i] += (r * 10 + a[i]) / b;
        r = (r * 10 + a[i]) % b;
    }
    c.flatten(a.len_);
    return c;
}

每次将上一次的余数乘10后加上当前的低位，再做除法即可