考点
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include <bits/stdc++.h>
using namespace std;
const int LEN = 5050;
class BigInt
{
public:
int len_;
int arr_[LEN];
int &operator[](int idx)
{
return arr_[idx];
}
BigInt(string s = "")
{
memset(arr_, 0, sizeof(arr_));
len_ = s.length();
for (int i = 1; i <= len_; ++i)
{
arr_[i] = s[len_ - i] - '0';
}
}
void flatten(int len)
{
len_ = len;
for (int i = 1; i <= len_; ++i)
{
if (arr_[i] >= 10)
{
arr_[i + 1] += arr_[i] / 10;
arr_[i] %= 10;
}
}
while (!arr_[len_])
--len_;
}
void print()
{
for (int i = max(1, len_); i >= 1; --i)
{
cout << arr_[i];
}
}
};
BigInt operator*(BigInt a, BigInt b)
{
BigInt c;
for (int i = 1; i <= a.len_; ++i)
{
for (int j = 1; j <= b.len_; ++j)
{
c[i + j - 1] += a[i] * b[j];
}
}
c.flatten(a.len_ + b.len_);
return c;
}
int main()
{
string a, b;
cin >> a >> b;
(BigInt(a) * BigInt(b)).print();
return 0;
}
|
思路
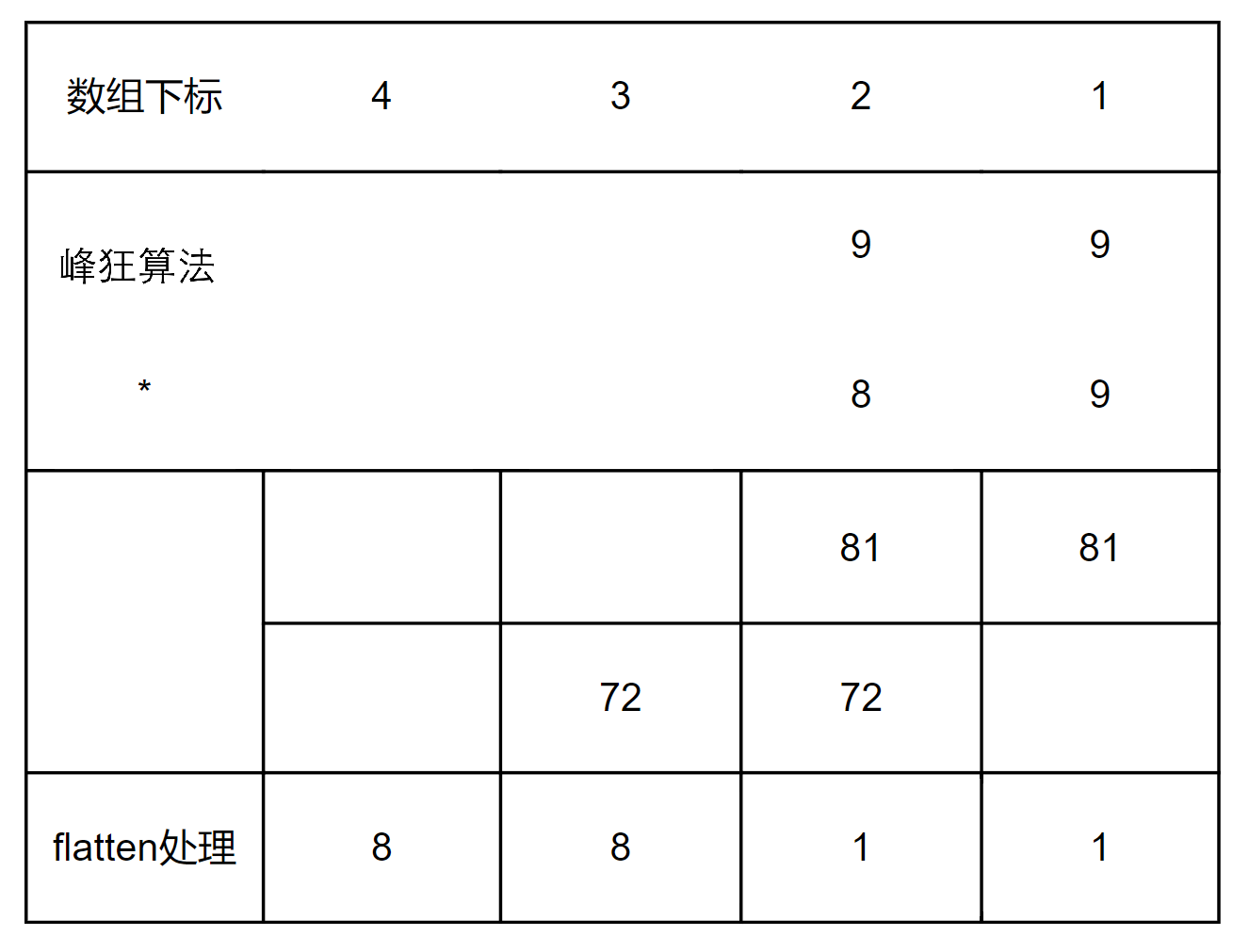
与高精度加法唯一的不同点,就在于按位处理上
可以发现,操作数a的处理位下标 + 操作数b的处理位下标 - 1 = 结果位下标
还需要牢记,乘法的结果位数不会超过两个操作数的位数之和