477. 汉明距离总和

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 488 阅读时长 ≈ 2 分钟

考点

  • 状态压缩
  • 排列组合
  • 异或技巧

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
	public:
		int totalHammingDistance(vector<int>& nums) {
			int ans = 0, size = nums.size();
			for (int i = 0; i < 31; i++) {
				int oneCnt = 0, mask = 1 << i;
				for (int j = 0; j < size; j++) {
					if (nums[j] & mask) oneCnt++;
				}
				ans += oneCnt * (size - oneCnt);
			}
			return ans;
		}
};

时间复杂度：\(O\left( C\cdot n \right)\)，在这里\(C\)常数等于31

空间复杂度：\(O\left( 1 \right)\)

思路

本题是461. 汉明距离的升级版，如果按照普通思路，数组内的元素两两异或再计算1个数，时间复杂度高达\(O\left( n^2 \right)\)

题目规定所有整数都是int类型的32位正数；若能求出所有元素对应的每一比特位集合的汉明距离，将它们累加求和即可得到答案

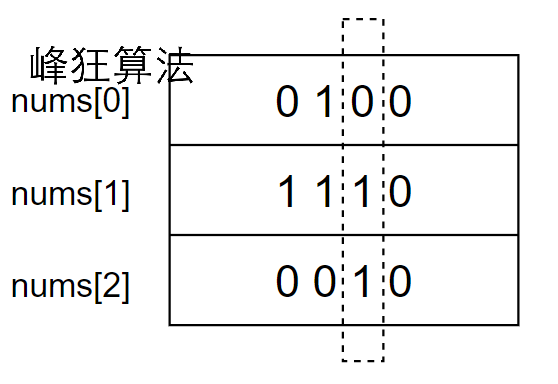
如下图所示，我们分别求出

  • nums[0]、nums[1]、nums[2]三个元素的第一比特位集合，即{0,0,0}的汉明距离，在这里是0
  • nums[0]、nums[1]、nums[2]三个元素的第二比特位集合，即{0,1,1}的汉明距离，在这里是2
  • nums[0]、nums[1]、nums[2]三个元素的第三比特位集合，即{1,1,0}的汉明距离，在这里是2
  • nums[0]、nums[1]、nums[2]三个元素的第四比特位集合，即{0,1,0}的汉明距离，在这里是2
  • 最后将它们累加求和，0 + 2 + 2 + 2 = 6，得到最终答案

如何求某一比特位集合的汉明距离呢？这里需要用到状态压缩这一思想

假设有比特位集合{0,1,1,1,0,0}

将其分成{0,0,0}和{1,1,1}两个子集合，对应元素命名为\(\left\{ a_0,a_1,a_2 \right\}\)、\(\left\{ b_0,b_1,b_2 \right\}\)，有如下算式：

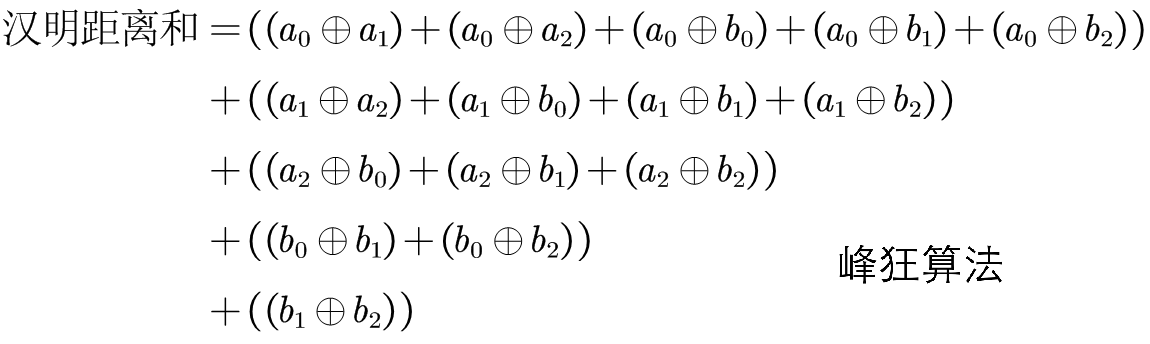
因为同一子集合内的值都相同，相互异或值恒为0，算式简化为：

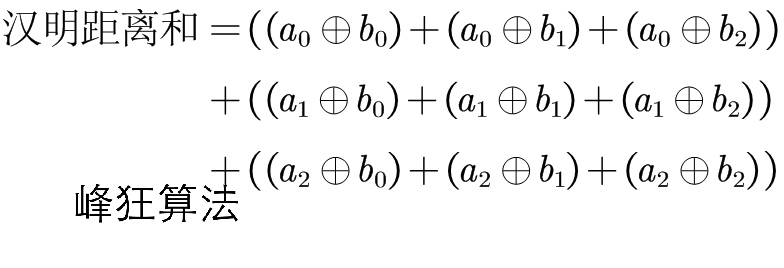
故而只需求出比特位集合中1与0的个数，并令其相乘，即可得到比特位集合的汉明距离