191. 位1的个数

发表于 分类于 阅读次数： Waline： 本文字数： 1k 阅读时长 ≈ 3 分钟

考点

  • n & (n - 1)技巧，即Brian Kernighan算法

  • n & -n技巧

  • 掩码技巧

  • 移位技巧

  • 位运算与分治法的综合

  • bitCount的实现

  • lowBit的实现

题解

同下

思路

有若干方法可以实现bitCount，下面依次列举，便于快速熟悉位运算的各种技巧

掩码计数

最容易想到的办法，就是使用类似计算机网络中的掩码，与原数逐位比较；这里的掩码也必须为无符号32位类型，否则会溢出

对于int来说，

正数极值用二进制表达是0111_1111_1111_1111_1111_1111_1111_1111

负数极值用二进制表达是1000_0000_0000_0000_0000_0000_0000_0000

负数以补码的形式存在，-1用二进制表达是1111_1111_1111_1111_1111_1111_1111_1111

1
2
3
4
5
6
7
8
9
10
11
class Solution {
	public:
		int hammingWeight(uint32_t n) {
			int cnt = 0;
			uint32_t mask = 1;
			for (int i = 0; i <= 31; mask = mask << 1, i++) {
				if (n & mask) cnt++;
			}
			return cnt;
		}
};

时间复杂度：\(O\left( k \right)\)，其中\(k\)为uint32_t的位数，在这里是32位

空间复杂度：\(O\left( 1 \right)\)

右移计数

每次判断最低位是否为1，然后将原数右移一位；因为题目说明了原数是无符号32位，所以右移不会新增1的个数

若是负数，右移时高位会补1

1
2
3
4
5
6
7
8
9
10
11
class Solution {
	public:
		int hammingWeight(uint32_t n) {
			int cnt = 0;
			while (n) {
				cnt += n & 1;
				n = n >> 1;
			}
			return cnt;
		}
};

时间复杂度：\(O\left( k \right)\)，其中\(k\)为uint32_t的位数，在这里是32位

空间复杂度：\(O\left( 1 \right)\)

Brian Kernighan算法

对于任何一个数n，n & (n - 1)能够将最低位的1变为0

1
2
3
4
5
6
7
8
9
10
11
class Solution {
	public:
		int hammingWeight(uint32_t n) {
			int cnt = 0;
			while (n) {
				n &= n - 1;
				cnt++;
			}
			return cnt;
		}
};

时间复杂度：\(O\left( \log n \right)\)，循环次数等于\(n\)的二进制位中1的个数

空间复杂度：\(O\left( 1 \right)\)

lowBit

对于任何一个数n，n & -n能够获取最低位的1的位置；假设二进制表达为0110，则lowBit返回0010

1
2
3
4
5
6
7
8
9
10
11
class Solution {
	public:
		int hammingWeight(uint32_t n) {
			int cnt = 0;
			while (n) {
				n -= n & -n;
				cnt++;
			}
			return cnt;
		}
};

时间复杂度：\(O\left( \log n \right)\)，循环次数等于\(n\)的二进制位中1的个数

空间复杂度：\(O\left( 1 \right)\)

分治

参考JDK中Integer.bitCount的函数原型

1
2
3
4
5
6
7
8
9
10
11
class Solution {
	public:
		int hammingWeight(uint32_t n) {
			n = (n & 0x55555555) + ((n >> 1) & 0x55555555);
			n = (n & 0x33333333) + ((n >> 2) & 0x33333333);
			n = (n & 0x0f0f0f0f) + ((n >> 4) & 0x0f0f0f0f);
			n = (n & 0x00ff00ff) + ((n >> 8) & 0x00ff00ff);
			n = (n & 0x0000ffff) + ((n >> 16) & 0x0000ffff);
			return n;
		}
};

原理类似归并排序的迭代版，每次按照单位长度进行归并：

  1. 单位长度为1时，1个数取决于其本身是否为1
  2. 单位长度为2，取相邻高低位，它们各自的1个数相加，达到一一归并为二的效果
  3. 单位长度为4，取相邻且单位长度为2的两部分，它们各自的1个数相加，达到二二归并为四的效果
  4. 单位长度为8，取相邻且单位长度为4的两部分，它们各自的1个数相加，达到四四归并为八的效果
  5. 循环同上

假设需要统计二进制序列1011101110中1的总数，分治过程如下

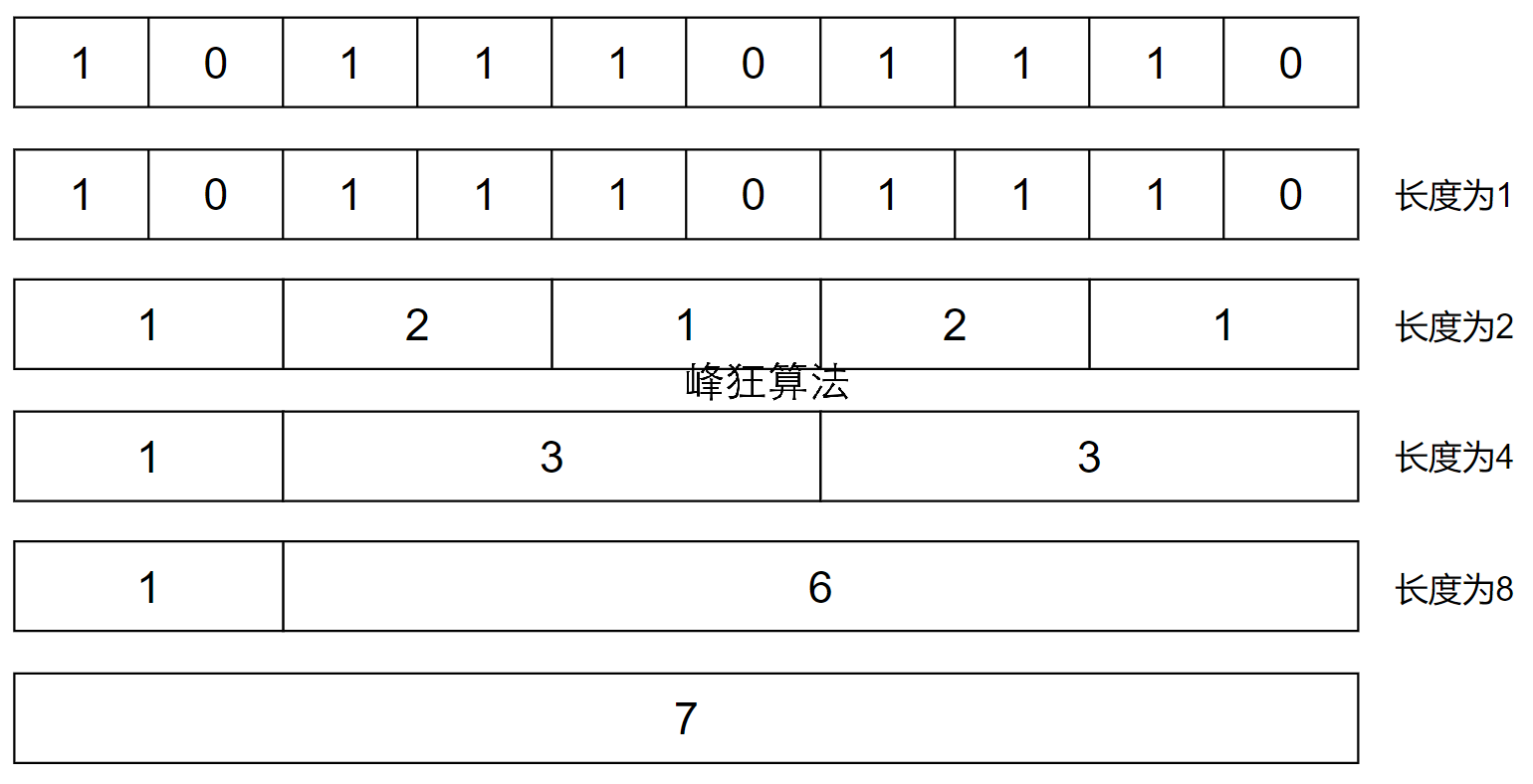
假设有二进制1110，求1的个数\(N\)；设二进制位编号从左到右分别为a、b、c、d，那么有 \[ N=N_a+N_b+N_c+N_d=N_{a,b}+N_{c,d} \] 初始单位长度为1，按上面的分治过程，需要一一组合为二

在第一步中，设计掩码0101，令0101 & 1110 = 0100取出\(N_b\)和\(N_d\)

再1110 >> 1 = 0111，0101 & 0111 = 0101取出\(N_a\)和\(N_c\)

0100 + 0101 = 1001就能得到\(N_{a,b}\)与\(N_{c,d}\)

第二步中可以设计0011这一掩码，1001 & 0011 = 0001取出\(N_{c,d}\)

1001 >> 2 = 0010，0010 & 0011 = 0010取出\(N_{a,b}\)

0001 + 0010 = 0011 = 十进制的3，即为 \[ N=N_{a,b}+N_{c,d} \] 那么这些掩码的功效你应该能明白了

1
2
3
4
5
0x55555555  ‭0b01010101010101010101010101010101‬
0x33333333  ‭0b00110011001100110011001100110011‬
0x0f0f0f0f  ‭0b00001111000011110000111100001111‬
0x00ff00ff  0b00000000111111110000000011111111
0x0000ffff  ‭0b00000000000000001111111111111111‬

时间复杂度：\(O\left( \log C \right)\)，其中\(C\)为uint32_t的位数，在这里是32位；大部分情况下，是所有方法中最快的一个

空间复杂度：\(O\left( 1 \right)\)