148. 排序链表

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 993 阅读时长 ≈ 3 分钟

考点

  • 链表的排序

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
	private:
		ListNode* MergeList(ListNode* l1, ListNode* l2) {
			if (l1 == nullptr) return l2;
			if (l2 == nullptr) return l1;
			if (l1->val < l2->val) {
				l1->next = MergeList(l1->next, l2);
				return l1;
			} else {
				l2->next = MergeList(l1, l2->next);
				return l2;
			}
		}

		ListNode* MergeSort(ListNode* head) {
			ListNode *dummyHead = new ListNode(-1, head), *cur = dummyHead;
			int len = 0;
			while (cur->next != nullptr) {
				cur = cur->next;
				len++;
			}

			for (int subLen = 1; subLen < len; subLen *= 2) {
				ListNode *curNew = dummyHead, *cur = dummyHead->next;
				while (cur != nullptr) {
					ListNode *leftHead = cur;
					for (int i = 1; i < subLen && cur->next != nullptr; cur = cur->next, i++);
					ListNode *rightHead = cur->next;
					cur->next = nullptr;
					cur = rightHead;
					for (int i = 1; i < subLen && cur != nullptr && cur->next != nullptr; cur = cur->next, i++);
					if (cur != nullptr) {
						ListNode *nextLeftHead = cur->next;
						cur->next = nullptr;
						cur = nextLeftHead;
					}
					curNew->next = MergeList(leftHead, rightHead);
					while (curNew->next != nullptr) curNew = curNew->next;
				}
			}
			return dummyHead->next;
		}

	public:
		ListNode* sortList(ListNode* head) {
			return MergeSort(head);
		}
};

思路

题目要求在O(nlogn) 时间复杂度和常数级空间复杂度下对链表进行排序

考虑时间复杂度，满足要求的有归并排序、堆排序与快速排序；后两者在链表实现上较难，所以选择归并排序

首先写出递归版本的归并排序，思路很简单

  1. 在递归的去方向中：每次找到链表的中点，并利用递归分割成左子链表和右子链表
  2. 在递归的回方向中：合并左右子链表；因为子链表均有序，可以参考21. 合并两个有序链表代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
	private:
		ListNode* MergeList(ListNode* l1, ListNode* l2) {
			if (l1 == nullptr) return l2;
			if (l2 == nullptr) return l1;
			if (l1->val < l2->val) {
				l1->next = MergeList(l1->next, l2);
				return l1;
			} else {
				l2->next = MergeList(l1, l2->next);
				return l2;
			}
		}

		ListNode* MergeSort(ListNode* head) {
			//很重要，否则会导致MergeSort函数死循环
			if (head == nullptr || head->next == nullptr) return head;
			ListNode *slow = head, *fast = slow;
			while (fast->next != nullptr && fast->next->next != nullptr) {
				slow = slow->next;
				fast = fast->next->next;
			}
			ListNode *newHead = slow->next;
			slow->next = nullptr;
			return MergeList(MergeSort(head), MergeSort(newHead));
		}

	public:
		ListNode* sortList(ListNode* head) {
			return MergeSort(head);
		}
};

但递归是自顶向下的写法，显然空间复杂度是O(logn)并不满足题目需求；所以需要使用自底向上的写法

递归的去方向不断地拆分链表，故而消耗了额外的栈空间；若用迭代来替代递归的拆分动作，就不会有额外的空间损耗

自底向上的迭代思路如图所示，其中有序子链表合并操作的代码直接参考21. 合并两个有序链表即可

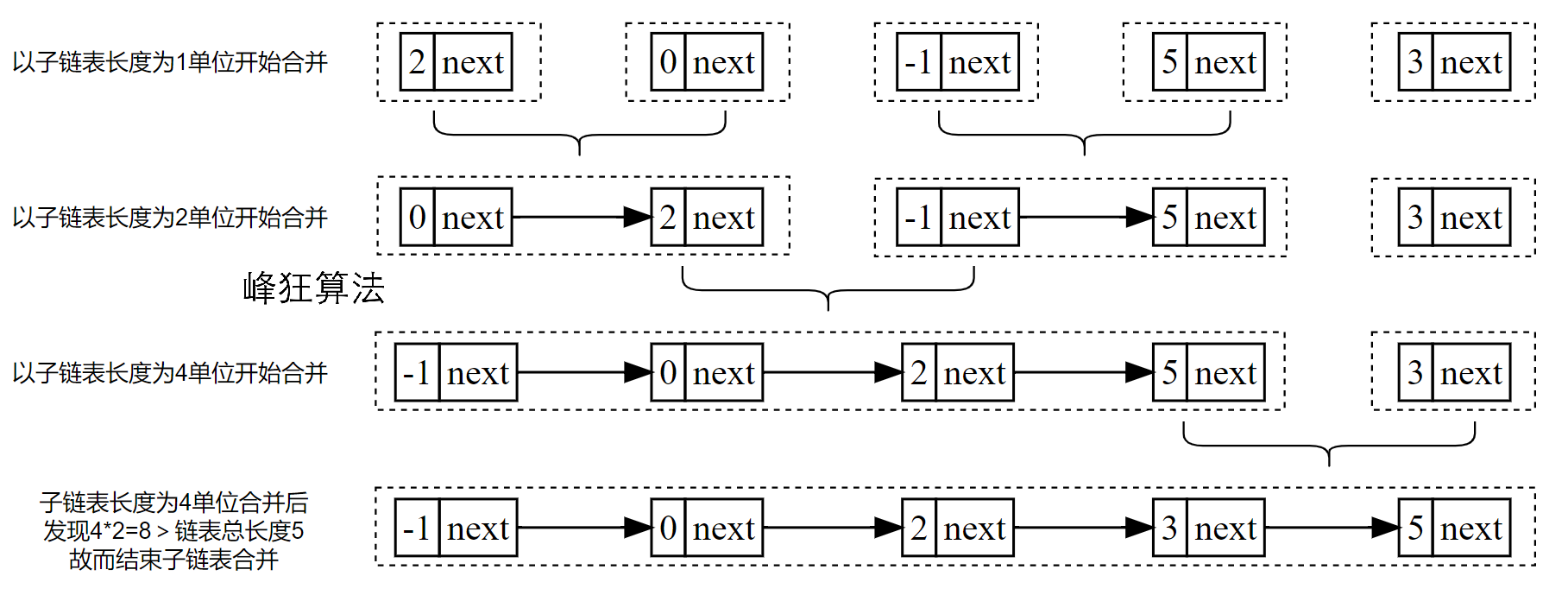
编程如下，为了可读性部分逻辑有重复，简化后就是题解代码的模样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
	private:
		ListNode* MergeList(ListNode* l1, ListNode* l2) {
			if (l1 == nullptr) return l2;
			if (l2 == nullptr) return l1;
			if (l1->val < l2->val) {
				l1->next = MergeList(l1->next, l2);
				return l1;
			} else {
				l2->next = MergeList(l1, l2->next);
				return l2;
			}
		}

		ListNode* MergeSort(ListNode* head) {
			ListNode *dummyHead = new ListNode(-1, head), *cur = dummyHead;
			int len = 0;
			while (cur->next != nullptr) {
				cur = cur->next;
				len++;
			}

			//外循环是待合并的子链表长度，初始为1，每次乘2
			//子链表的长度*2肯定小于等于总长度
			//当然，子链长度等于总长度的时候就没必要自己合并自己，所以这里只有小于号没有等于号
			for (int subLen = 1; subLen < len; subLen *= 2) {
				//每次都从头开始更新链表
				ListNode *curNew = dummyHead, *cur = dummyHead->next;
				//按照归并的规律，两个子链表一组
				while (cur != nullptr) {
					//记录左子链表头
					ListNode *leftHead = cur;
					//寻找左子链表尾
					for (int i = 1; i < subLen && cur->next != nullptr; cur = cur->next, i++);
					//左子链表尾的下一个节点为空，说明没有右子链表，即到了整个大链表的尾部
					//那么合并完后直接开启新的大循环
					if (cur->next == nullptr) {
						curNew->next = leftHead;
						cur = nullptr;
					} else {
						//若存在右子链表
						//记录右子链表头
						ListNode *rightHead = cur->next;
						//左子链表尾部断开，使其成为单独的链表便于合并
						cur->next = nullptr;
						//寻找右子链表尾
						cur = rightHead;
						for (int i = 1; i < subLen && cur->next != nullptr; cur = cur->next, i++);
						ListNode *nextLeftHead = cur->next;
						//右子链表尾部断开
						cur->next = nullptr;
						cur = nextLeftHead;
						//塞入左右子链表合并后的新链表
						curNew->next = MergeList(leftHead, rightHead);
						while (curNew->next != nullptr) curNew = curNew->next;
					}
				}
			}
			return dummyHead->next;
		}

	public:
		ListNode* sortList(ListNode* head) {
			return MergeSort(head);
		}
};