142. 环形链表 II

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 588 阅读时长 ≈ 2 分钟

考点

  • 快慢指针/双指针
  • 链表的环

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
	public:
		ListNode *detectCycle(ListNode *head) {
			ListNode *slow = head, *fast = head;
			while (fast != nullptr) {
				slow = slow->next;
				fast = fast->next;
				if (fast != nullptr) fast = fast->next;
				if (fast != nullptr && slow == fast) {
					ListNode *slow = head;
					while (slow != fast) {
						slow = slow->next;
						fast = fast->next;
					}
                    //这里换成slow是一样的
					return fast;
				}
			}
			return nullptr;
		}
};

思路

我曾在141. 环形链表的题解中阐述了如何用快慢指针判断链表是否存在环，本题是其升级版，要寻找环的入口

我们已知链表头，能求得相遇点，现在要找到环入口，绘图如下

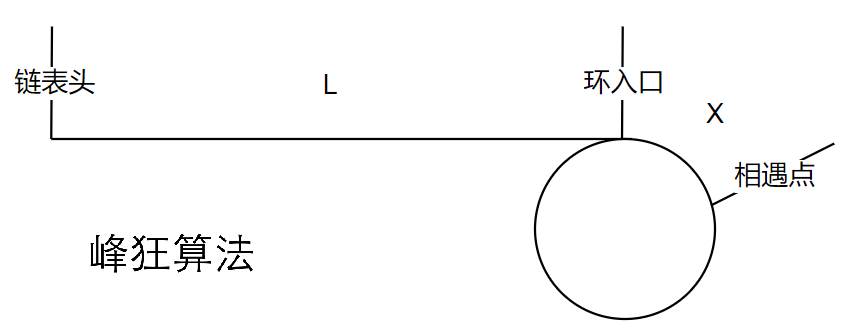
通式

根据快指针移动速度是慢指针移动速度的两倍这一性质，可以得到以下通式 \[ \underset{\text{慢指针到达相遇点所需时间}}{\underbrace{\frac{L+m\times C+X}{1}}}=\underset{\text{快指针到达相遇点所需时间}}{\underbrace{\frac{L+n\times C+X}{2}}} \] 解释如下

L：链表头到环入口的距离

X：环入口到相遇点的距离

C：环的周长

m，n：未知数，各指针绕环次数

两个未知数是无法编程的，可以优化一下

慢指针在环内第一圈就能与快指针重合

慢指针达到环入口时，假设快指针与慢指针的相对距离长度为M

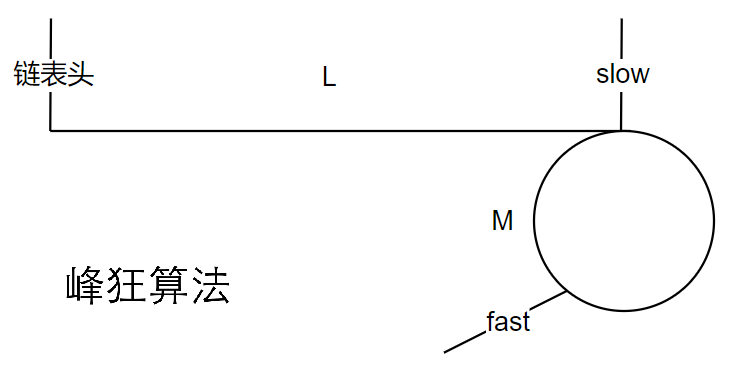
显然，M必小于周长C

根据141. 环形链表的题解中提到的相遇时间公式，能得到下面不等式；代表慢指针在进入环内的第一圈就与快指针相遇了 \[ \underset{\text{相遇时间}}{\underbrace{\frac{M}{2-1}}}<\underset{\text{慢指针绕环一次的时间}}{\underbrace{C=\frac{C}{1}}} \] 所以，通式可以优化为 \[ \underset{\text{慢指针到达相遇点所需时间}}{\underbrace{\frac{L+X}{1}}}=\underset{\text{快指针到达相遇点所需时间}}{\underbrace{\frac{L+n\times C+X}{2}}} \]

实现

通式变形，可以得到 \[ 2\times \left( L+X \right) =L+n\times C+X \]

\[ L=n\times C-X \]

\[ L=\left( n-1 \right) \times C+\left( C-X \right) \]

最终通式的含义可以这么理解

某指针A从链表头出发

某指针B同时从相遇点出发，先走过C-X个单位到达环入口，再绕环n-1次

最终两个指针将在环入口相遇

再结合题解的源码看，就一目了然了