141. 环形链表

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 548 阅读时长 ≈ 2 分钟

考点

  • 快慢指针
  • 链表的环

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
	public:
		bool hasCycle(ListNode *head) {
			ListNode *slow = head, *fast = head;
			while (fast != nullptr) {
				slow = slow->next;
				fast = fast->next;
				if (fast != nullptr) fast = fast->next;
				if (fast != nullptr && fast == slow) return true;
			}
			return false;
		}
};

思路

判断链表中是否存在环，需要用到快慢指针

令slow为慢指针，每次移动一个单位；令fast为快指针，每次移动两个单位

两个指针同时移动，若相遇且fast不为nullptr时，即存在环

为什么快慢指针可以解决

如果不存在环，快指针肯定将慢指针远远抛在身后

一旦存在环，快指针会比慢指针更早到达环内，并且在环内无限循环

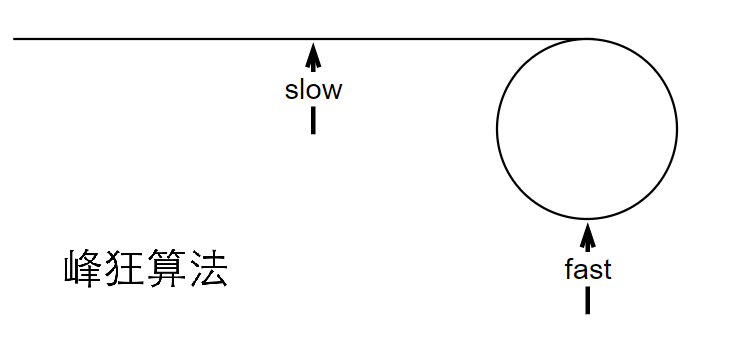
如果慢指针也进入环内，那么就变成追击问题了，或者俗称的龟兔赛跑数学题

如图所示，快慢指针都是顺时针移动；若两指针距离X，环周长为C，那么快指针需要移动C-X个相对距离长度才能相遇

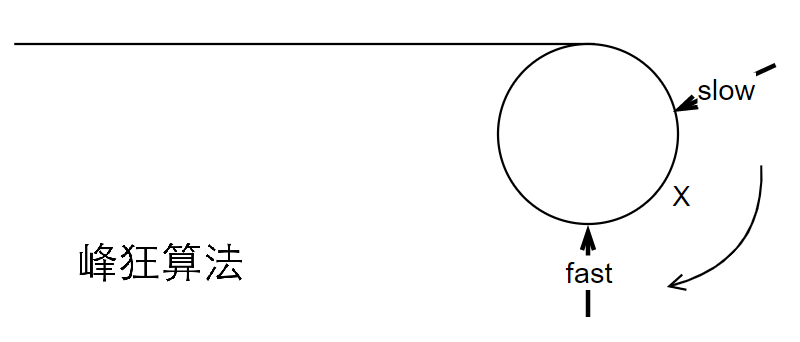
追击问题中，有以下常识： \[ \text{相对速度}=\text{速度差} \]

\[ \text{相遇时间}=\frac{\text{相对距离长度}}{\text{相对速度}} \]

所以，再经过\[ \frac{C-X}{2-1} \]次移动后，快慢指针就可以相遇了

为什么快指针每次移动两个单位

正如刚才提到的相遇时间计算公式，我们必须保证相对距离长度可以被相对速度整除才能相遇

因为在具体的程序实现上，所谓的相遇时间其实就是循环次数，不可能为小数；若取两个单位，相对速度就是1，任何数都可以被1整除

所以，快指针每次移动也可以取三个单位，四个单位，五个单位....但是不一定可以整除相对距离长度

如果相遇时间是小数，说明两个指针会错过而永不相遇

快指针移动单位 慢指针移动单位 相对速度 相对距离长度 相遇时间
2 1 1 4/5 4/5
3 1 2 4/5 2/2.5
4 1 3 11/15 3.67/5